Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.6 - Ex. 60b
Encontre o valor exato de cada expressão.
60.(a) (b)
Passo 1
O problema pede pra a gente calcular,o valor exato de ! Pra isso temos que ter em mente que:
Aqui, basta que a gente calcule esses valores lembrando que uma função trigonométrica elevada a “-1” é na verdade outra forma de escrever as funções arco-trigonométricas.
Assim, temos que:
Ou seja, queremos determinar o arco (ângulo) cuja secante vale 2.
E a secante de um ângulo qualquer, você sabe, é o inverso do cosseno. Assim:
Passo 2
Queremos então um arco que valha o seguinte:
Assim, fica mais fácil. Multiplicando cruzado essa fração, teremos:
Agora, qual ângulo você lembra cujo cosseno vale 0,5?
Mas não é o único ângulo cujo o cosseno vale . Se liga no círculo trigonométrico:
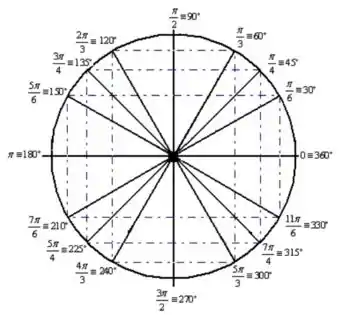
De cara a gente vê que tem o mesmo cosseno. Então podemos escrever a seguinte relação:
Na verdade, todos os arcos que obedecem a seguinte relação valem como resposta:
Onde é um número inteiro qualquer (0,1, 2, -1, -2, 1000, etc.). Ou seja, podemos ter:
Isso quer dizer, todos os arcos côngruos ao de serão possíveis respostas pra .