Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.4 - Ex. 7c

Encontre valores aproximados da solução do problema de valor inicial dado em t = 0,5; 1,0; 1,5 e 2,0, usando o método especificado. Para os valores iniciais, use os valores dados pelo método de Runge-Kutta; veja os Problemas de 7 a 12 da Seção 8.3. Compare os resultados dos vários métodos entre si e com a solução exata (se disponível).

Use o método inverso de diferenciação de quarta ordem com h = 0,05.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nessa questão, vamos trabalhar com o erro associado ao método Runge-Kutta. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser determinar o formato da solução de previsão.

y n + 1 = 1 25   48 y n - 36   y n - 1 + 16 y n - 2 - 3 y n - 3 + 12 h f n + 1

f n + 1 = ( t n + 1   , y n + 1   )

y n + 1 = 1 25   48 y n - 36   y n - 1 + 16 y n - 2 - 3 y n - 3 + 12 h ( t n + 1 2 - y n + 1 ) 2 sin ⁡ y n + 1

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Aplicando o método inverso, teremos:

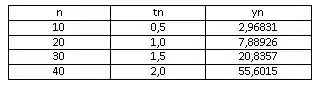
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 6, determine os intervalos nos quais existem, com certeza, soluções.1. y ( 4 ) + 4 y ' ' ' + 3 y = t
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular. y ″ + ( ln ⁡ | x | ) y ' + 3 x y=0
Encontre valores aproximados da solução do problema de valor inicial dado em t = 0,5; 1,0; 1,5 e 2,0, usando o método especificado. Para os valores iniciais, use os valores dados pelo método de Runge-
Encontre valores aproximados da solução do problema de valor inicial dado em t = 0,5; 1,0; 1,5 e 2,0, usando o método especificado. Para os valores iniciais, use os valores dados pelo método de Runge-