Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 38
- Se , encontre .
- Verifique se sua resposta em (a) é razoável, comparando os gráficos de e .
Passo 1
E aí, galerinha, tudo joia do lado daí?
Se liga só nessa questão, no item a) o enunciado nos dá a função
E pede para encontrarmos a derivada de , aqui usaremos a seguinte regra do quociente:
Ou seja, temos:
E no item b) vamos comparar os gráficos de e . A ideia aqui é verificar se a resposta faz sentido utilizando nossos conhecimentos do comportamento de uma derivada.
Passo 2
Aqui no item a), vamos encontrar a derivada de
Bom, precisamos derivar esta função. Antes de tudo devemos notar que há uma divisão entre os termos. Então o que usamos?
A Regra do Quociente, certo? Vamos lembrar:
Se chamarmos:
e
Derivando:
Substituindo:
Se isolarmos :
E pronto! Terminamos a letra a, e agora vamos para a b!
Passo 3
As funções obtidas são:
E
Logo, o gráfico é representado abaixo.
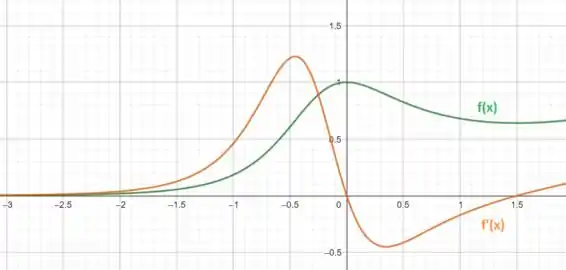
A derivada nos mostra a inclinação da reta tangente ao gráfico da função. Então, pelo gráfico, quando a derivada é positiva, a reta tangente tem inclinação crescente e, consequentemente, a função também cresce. Quando a inclinação diminui, a função decresce. A derivada intercepta o eixo x duas vezes.