Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios adicionais e avançados - Ex. 2
Encontre o vértice, o foco e a diretriz da parábola:
Passo 1
Vem comigo pessoal!!
Relembrando que uma parábola é um conjunto que consiste de todos os pontos em um plano equidistantes de um ponto fixo e de uma dada reta fixa no plano. O ponto fixo é o foco da parábola. A reta fixa é a diretriz.
A equação genérica da parábola é dada por:
Onde o vértice é .
No nosso exercício temos a seguinte equação:
Rearranjando essa equação, temos:
Dessa equação já conseguimos obter o vértice:
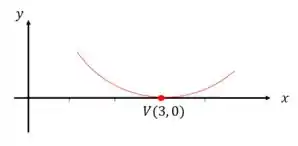
Sabemos que nossa curva terá concavidade para cima, por conta do valor positivo e o quadrado ser em relação a . Então, já temos no nosso gráfico os seguintes dados:
Passo 2
Também conseguimos encontrar o valor de , porque:
Como vimos no Passo 1 que a concavidade é para cima, logo a diretriz será , logo:
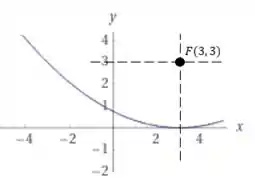
Com o valor de , sabemos que o foco será 3 unidades para acima, assim como a diretriz foi 3 unidades para baixo, ou seja:
Tchau pessoal.
Resposta
- Vértice ;
- Foco ;
- Diretriz .