O que é uma elipse? Quais são as equações cartesianas para elipses centradas na origem com focos em um dos eixos coordenados? Como você pode determinar os focos, vértices e diretrizes de tal elipse a partir de sua equação?

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

Uma elipse é o conjunto de todos os pontos em um plano tal que a soma de suas distâncias a dois pontos fixos é uma constante. Cada ponto fixo é chamado de foco da elipse. Toda elipse tem dois eixos de simetria. O eixo maior é chamado de eixo maior, e o eixo menor é chamado de eixo menor. Cada ponto final do eixo maior é o vértice da elipse, e cada ponto final do eixo menor é um co-vértice da elipse. O centro de uma elipse é o ponto médio dos eixos maior e menor. Os eixos são perpendiculares no centro. Os focos sempre estão no eixo maior, e a soma das distâncias dos focos a qualquer ponto da elipse é maior que a distância entre os focos.

A forma padrão da equação de uma elipse com centro e eixo principal paralelo ao eixo é:

onde .

O comprimento do eixo maior é .

As coordenadas dos vértices são.

O comprimento do eixo menor é .

As coordenadas dos co-vértices são .

As coordenadas dos focos são , onde .

Conforme na figura abaixo:

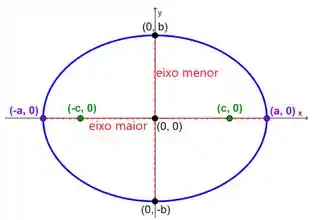
Já a forma padrão da equação de uma elipse com centro e eixo principal paralelo ao eixo é:

onde .

O comprimento do eixo maior é .

As coordenadas dos vértices são.

O comprimento do eixo menor é .

As coordenadas dos co-vértices são .

As coordenadas dos focos são , onde .

Conforme na figura abaixo:

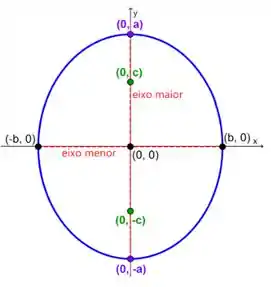
Espero ter ajudado! Abraços e até a próxima!