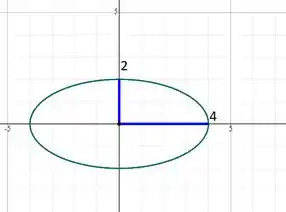
Encontre os vértices e os focos da elipse e esboce o seu gráfico.

Oieeee, tudo bem com você? Vamos resolver essa atividade hoje.

Nessa questão, nos foi dada a equação de uma elipse, para encontrarmos seus vértices e focos. A nossa elipse é a seguinte:

Observe que como não temos nenhum número somando ou subtraindo do e do podemos dizer que a elipse é centrada na origem.

A equação geral de uma elipse centrada na origem é

e quando temos o número maior embaixo do esta é uma elipse com eixo maior no eixo .

O foco de uma elipse desse tipo é dado por

Os vértices de uma elipse centradas na origem e com são:

Para desenharmos esse tipo de elipse podemos seguir o gráfico a seguir:

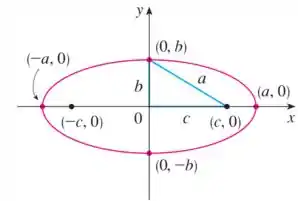
Em que e como você pode notar é o foco.