Encontre os vértices e os focos da elipse e esboce seu gráfico
16-
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade. A gente tem a equação da elipse:
E a partir dela a gente precisa encontrar o foco e os vértices. Vamos fazer isso utilizando a equação geral da elipse.
O foco está em:
E o vértice:
E
Então comparando a nossa equação a geral, a gente consegue resolver essa atividade aqui.
Essa elipse tem a cara de uma elipse que está com centro fora da origem. E uma função desse tipo tem a seguinte cara:
Então temos que arrumar o que está escrito no enunciado até ficar com essa forma. Vamos tentar organizar com e com .
Passo 2
Agora vem o bizu monxtro da questão. Nós temos que forças um produto notável com e outro produto notável com e com isso somar os dois lados da equação com o fator que falta para formar um produto notável perfeito:
Começando com nós conseguimos ver que é muito parecido com:
Logo basta somar um nos dois lados.
Agora para podemos ver que se assemelha muito com:
Então basta somar aos dois lados.
Não sei se vocês perceberam, mas uma equação do tipo:
Está próximo de uma equação:
Passo 3
Logo vamos somar e na equação
Dividindo a equação por temos:
Está da forma que deveria estar!
Passo 4
Com essa equação percebemos que a elipse tem centro igual a:
Para encontrar esse valor basta zerar os numeradores das frações.
E tem valores de e iguais a:
Logo os vértices dessa elipse estarão em:
E
Não confundir, vai com e com .
E como então podemos dizer que o eixo maior da elipse estará no eixo x. Então os focos valerão:
Onde valerá:
Logo os focos estarão em:
Gráfico da função:
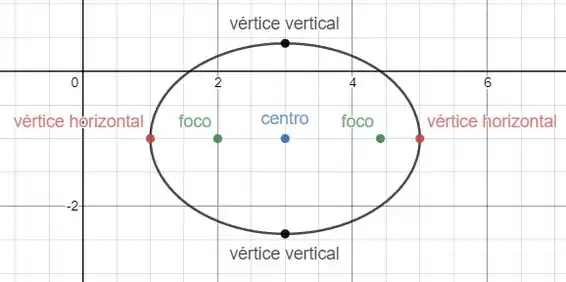
Resposta
Vértices horizontais:
Vértices verticais:
Foco: