Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Passo 1
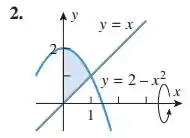
Queremos o volume de um sólido obtido quando giramos a área, entre (limitando por cima) e (limitando por baixo), em torno de . É só usarmos a fórmulinha:
Vamos começar!
Passo 2
Pela imagem vemos que:
Conseguimos visualizar que um dos extremos de integração é (a reta que limita a área pela direita), mas o outro precisamos achar, fazendo a intercessão entre as curvas:
Resolvendo essa equação, achamos:
Mas como pela figura, vemos que
Nossa integral fica então:
Passo 3
Agora é só calcular a integral:
Abrindo o produto notável: