Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.2 - Ex. 1
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
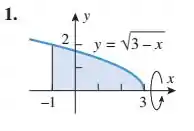
Passo 1
Queremos o volume de um sólido obtido quando giramos a área embaixo de em torno de . É só usarmos a fórmulinha:
Vamos começar!
Passo 2
Pela imagem vemos que:
E os extremos de integração são:
Nossa integral fica então:
Passo 3
Agora é só calcular a integral:
Resposta
Exercícios de Livros Relacionados
A base de um certo sólido é a região delimitada por y = 0 e x = 4 . Cada seção transversal perpendicular ao eixo x é um semicírculo, com diâmetro de um lado a outro da base. Encontre o volume do sólid
A ponta cônica de reentrada de um veículo espacial é desenhada de tal forma que uma seção transversal tomada x pés da ponta e perpendicular ao eixo de simetria é um círculo com raio de 1 4 x 2 pés. En
Encontre o volume do sólido que resulta quando a região do Exercício 43 for girada em torno da reta y = - 1 .
Encontre o volume do sólido cuja base é a região delimitada pelas curvas y = x e y = x 2 cujas seções transversais perpendiculares ao eixo x são quadrados.
Um certo sólido tem uma altura de 1m e uma seção transversal, tomada x metros acima da base do sólido, é uma região anular de raio interno x 2m e raio externo xm . Encontre o volume do sólido.