Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 63

Sabemos do exemplo 1 que a região R = x , y x ≥ 1 ,   0 ≤ y ≤ 1 / x } tem área infinita. Mostre que pela rotação de R em torno do eixo x obtemos um sólido com volume finito.

Passo 1

A questão pede para calcularmos o volume do sólido gerado pela rotação da região R (abaixo da curva y = 1 / x de x = 1 até infinito) em torno do eixo x .

Um exemplo de um disco para o método do disco é mostrado para x = 2

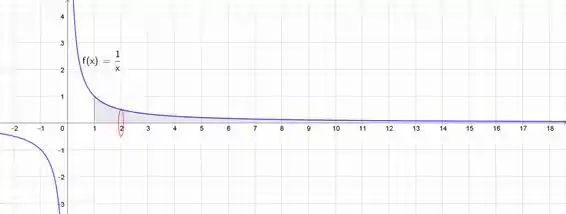
O raio do disco é r = 1 x

E a área do disco é A x = π r 2 = π x 2

Esse volume é descrito pela integral imprópria

V = ∫ 1 ∞ π r 2 d x ,

onde r é y como função de x . Assim,

V = π ∫ 1 ∞ 1 x 2 d x

Passo 2

Vamos ver se a integral imprópria converge calculando primeiro a integral ∫ 1 t 1 x 2 d x :

∫ 1 t 1 x 2 d x = - 1 x 1 t = 1 - 1 t

Fazendo t → ∞ , temos que

lim t → ∞ ⁡ ∫ 1 t 1 x 2 d x = lim t → ∞ ⁡ 1 - 1 t = 1

Assim,

∫ 1 ∞ 1 x 2 d x = 1

Portanto,

V = π ∫ 1 ∞ 1 x 2 d x = π

Resposta

π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 1 ≤ x ≤ 2 e 0 ≤ y ≤ x 3 - 1
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 1 ≤ x ≤ 4 e 1 ≤ y ≤ x
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ 8 e 0 ≤ y ≤ x 3
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 1 ≤ x ≤ e e 0 ≤ y ≤ l n x
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ π e 0 ≤ y ≤ sin ⁡ x