Exercícios de Volumes de Sólidos Infinitos - Lista de Exercícios Resolvida

Tendo em vista a área entras as funções abaixo:

Calcule o volume do sólido obtido na rotação dessa região em torno do eixo .

Calcule o volume do sólido de revolução obtido pela rotação da curva

Em torno do eixo .

Ao rotacionarmos em torno do eixo a região delimitada pela função , obtemos um sólido conhecido por Trombeta de Gabriel. No entando, ao girarmos em torno do eixo , obtemos um outro sólido conhecido como Vulcão de Descartes.

Calcule o volume do Vulcão de Descartes, para suficientemente grande, ou seja, .

Seja a região R limitada pelas curvas e .

a) Esboce R e calcule sua área

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

Seja R a região limitada pelas curvas e

a) Esboce R e calcule a sua área.

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

1. Seja a região do plano delimitada superiormente pelo gráfico de , à esquerda por e inferiormente pelo eixo . Seja o volume do sólido gerado pela rotação de em torno do eixo . Então:

1. é finito para todo .
2. não é finito para nenhum .
3. é finito apenas para .
4. é finito apenas para .

f x = 1 x - 1 x 2 , cujo gráfico está esboçado abaixo:

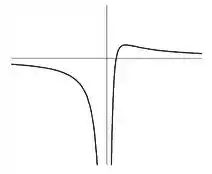
Sabendo que o eixo é uma assíntota horizontal do gráfico de , faça o que se pede.

1. Seja a região plana definida por

Calcule a área de e conclua que ela é infinita.

2. Seja o sólido obtido pela rotação da região em torno do eixo . Calcule o volume de .

Considere a região delimitada pelas curvas

a) Calcule a área da região

b) Calcule o volume do sólido obtido pela rotação da região em torno da reta .

Para uma função contínua o volume do sólido de revolução obtido pela rotação do seu gráfico em torno do eixo é dado por . Calcule esse volume no caso das funções indicadas abaixo.

, para , onde

Para uma função contínua o volume do sólido de revolução obtido pela rotação do seu gráfico em torno do eixo é dado por . Calcule esse volume no caso das funções indicadas abaixo.

, para , onde

Para uma função contínua o volume do sólido de revolução obtido pela rotação do seu gráfico em torno do eixo é dado por . Calcule esse volume no caso das funções indicadas abaixo.

, para , onde

Seja R a região limitada pelas curvas e

a) Esboce R e calcule a sua área.

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

Seja a região limitada pelas curvas e

a) Esboce R e calcule a sua área.

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

Determine o volume do sólido entre as esferas e e no interior da região cônica .

Seja a região limitada pelas curvas e

a) Esboce R e calcule a sua área.

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

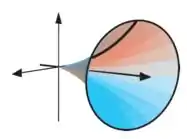
Para uma função contínua o volume do sólido de revolução obtido pela rotação do seu gráfico em torno do eixo é dado por

Calcule esse volume no caso em que , definida no intervalo , conforme a figura ao lado.

Ao rotacionarmos em torno do eixo a região delimitada pela função , obtemos um sólido conhecido por Trombeta de Gabriel. No entando, ao girarmos em torno do eixo , obtemos um outro sólido conhecido como Vulcão de Descartes.

Calcule o volume do Vulcão de Descartes, para suficientemente grande, ou seja, .

Seja a região entre as curvas e

Determine o volume do sólido obtido pela rotação de ao redor do eixo

Seja a região R limitada pelas curvas e .

a) Esboce R e calcule sua área

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

Considera-se a área entre a curva e o eixo para .

b) Determinar o volume do sólido de rotação, girando-se

b1) em torno da reta b2) em torno da reta

Consideremos a curva para .

b) Determinar a superfície do sólido de rotação, girando-se a curva em torno do eixo .