Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 5
Enfocando conceitos
Em cada parte, determine se a função definida pela tabela é injetora
Passo 1
Fala povo, tranquilo? Olha só, aqui a gente não tem a lei de formação bonitinha de . Então a tabela vai ter que ser o suficiente pra gente dizer se a função é injetora ou não. O truque vai ser olhar a correlação de com : se dois ou mais valores diferentes de tiverem o mesmo a função não será injetora. Bora checar?
Passo 2
Letra a)
Seja a tabela:
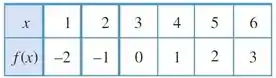
Vemos que nenhum valor de se repete para valores diferentes de , logo a função é injetora!
Passo 3
Letra b)
Seja a tabela:
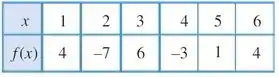
Vemos que o valor se repete para valores diferentes de :
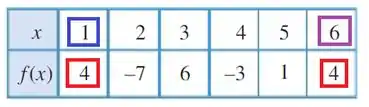
Portanto, nesse caso, a função é não injetora!
Resposta
- Injetora
- Não Injetora
Exercícios de Livros Relacionados
10. Faça o exercício 8 se x = c o s - 1 ( - 2 3 ) .8. b) t g( x )
Dado que x = s e n - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:7. e) c o s e c( x )
Nos Exercícios de 1 a 6, determine o valor funcional exato.6. a) c o s - 1 ( 1 )
Dado que x = s e n - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:7. d) s e c( x )
9. Faça o exercício 7 se x = s e n - 1 ( - 1 3 ) .7. c) c o t g( x )