Enfocando conceitos
A face de um relógio quebrado caiu inteira no plano com o centro do relógio na origem e as horas na direção do eixo positivo. Quando o relógio quebrou, a ponta do ponteiro das horas parou no gráfico de , onde é uma função que satisfaz .
- Existem algumas horas do dia que não podem ocorrer em tal configuração? Explique.
- Como é afetada sua resposta a se deve ser uma função invertível?
- Como são afetadas suas respostas a e se foi a ponta do ponteiro dos minutos que parou no gráfico de ?
Passo 1
Ok esse enunciado é esquisito a beça, mas vamos desmembrar ele. Primeiro, note o seguinte
- Relógio ta centrado na origem
- As 3 horas está na direção do eixo positivo
Usando essas configurações, podemos estabelecer esse sistema de coordenadas pro relógio:
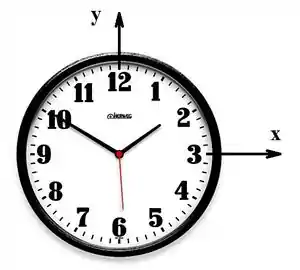
A questão diz também que o ponteiro das horas caiu em cima de uma função que passa na origem. Ou seja, os pontos e abaixo são pontos que necessariamente fazem parte de :
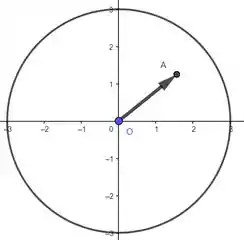
Mas olha só o doido: não sabemos exatamente onde é, mesmo sabendo que ele é um ponto da função. Por exemplo, podemos traçar uma função laranja que descreva o ocorrido
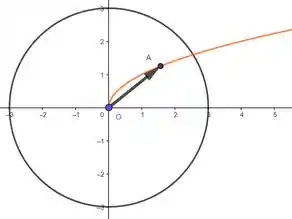
Quando a questão pergunta pra gente se existem algumas horas do dia que não podem ocorrer em tal configuração, o que ela quer saber na verdade é se é possível que o ponteiro continue sobre em outras horas. Nota a seguinte galera, como o ponteiro gira, ele descreve uma trajetória circular:
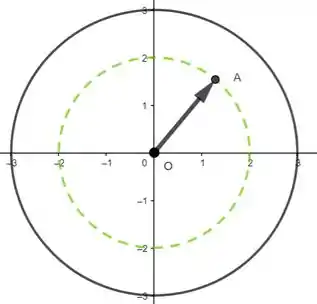
Portanto, a resposta da letra é sim se conseguirmos pensar em uma função que não somente tenha como uma verdade, mas também que corte a circunferência verde pelo menos duas vezes. Oras, é um bom exemplo de função que tem isso:
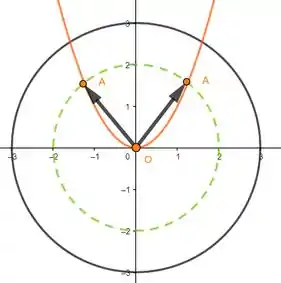
E tem outras funções também que são válidas! Teste e por exemplo!! Na verdade, nem precisa de uma lei de formação bonitinha, contanto que você trace uma curva que represente uma função corretamente e satisfaça as condições do enunciado, belezinha? Portanto a resposta da pergunta da letra é sim!
Passo 2
Agora vamos por mais condições pra e ver se isso muda alguma coisa. A nossa função agora é invertível. Será que muda alguma coisa? Bem, para uma função ser invertível, a gente sabe que ela deve ser bijetora. Outra coisa importantíssima é: toda função estritamente crescente ou decrescente em seu domínio é bijetora. Em resumo, nossa função deve:
- Conter
- Ser estritamente crescente ou decrescente
- Cortar a circunferência verde tracejada pelo menos duas vezes
Po galera, mesmo sem uma lei de formação bonitinha, não tem nada que impeça de uma função dessas existir! Por exemplo, se encaixa nesse perfil!
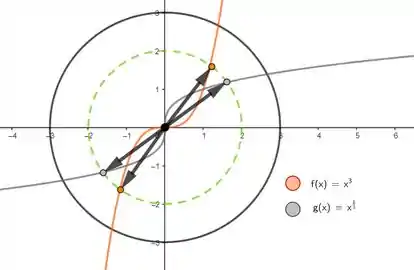
Veja que a inversa de também poderia ser uma função de exemplo pra letra em! No gráfico confirmamos que é inversa de pela simetria em relação ao eixo .
Passo 3
E pra fechar galera, a letra pergunta pra gente se alguma coisa mudaria se tudo tivesse acontecido com os ponteiros dos minutos. Bem, tudo que pensamos até aqui foi considerando “funções que cortem a circunferência tracejada verde”. Se o ponteiro fosse o dos minutos, a única diferença nas letras e seria que a circunferência verde e a preta coincidiriam. Pra letra a imagem ficaria:
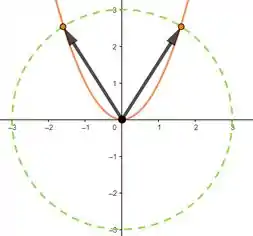
E pra :
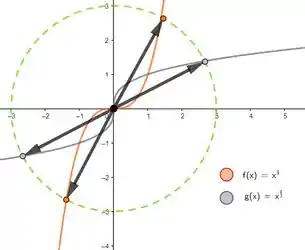
Portanto não, mudar o ponteiro não muda a resposta da letra a! Fechamos! Ufa
Resposta
- Para que o ponteiro das horas toque na função mais de uma vez ao girar, é necessário que a função seja capaz de cruzar com a circunferência que descreve a trajetória do ponteiro mais de uma vez. Existe uma variedade de funções que são capazes de fazer isso e conter o ponto também.
- A resposta da letra continua sendo sim se obrigarmos a ser uma função invertível
- A resposta da letra continua sendo sim se o ponteiro originalmente sobre fosse outro