Enfocando conceitos

1. Use um recurso computacional para calcular o valor de e e explique o que pode estar acontecendo no segundo cálculo.
2. Com quais valores de no intervalo seu recurso computacional produz um valor real para a função ?

Fala galera, tudo bem? Vamos lá! A questão já diz pra gente que tá valendo usar um recurso computacional, o que já é um grande ufa hahaha recomendo então uma famosa ferramenta de planilhas pra isso. Primeiro, vamos considerar:

Sendo assim, o que queremos na verdade é:

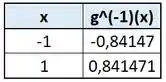
Pra e . Usando isso, vou montar uma tabelinha assim, usando a função “=ASEN()” do recurso computacional escolhido:

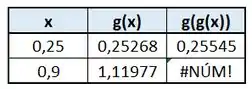
E olha só o que aconteceu. Pra , basicamente não mudamos o valor inserido quando fizemos . E a conta quando retorna “#NÚM!” é porque não achou um resultado. Em matematiquês, isso que dizer que não faz parte do domínio de . Ok, mas porque isso?

Bem galera, se temos, também temos:

E disso a gente tira duas informações importantes sobre a função :

• Como é u resultado de um seno, o domínio de deve ser os valores máximos e mínimos que um seno alcança, isto é:
• Como sai em radianos, a sua imagem deve ser os arcos responsáveis por esses valores máximos e mínimos de seno, logo:

Ou seja:

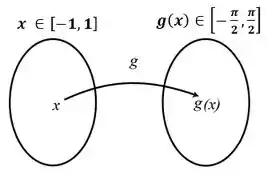
Porém quando fazemos

Obtemos também, ao inverter:

Note que, dessa vez, é o que é um seno! Sendo assim:

• Domínio de será os valores possíveis que um seno pode ter, logo:
• Imagem de será os valores dos arcos que geram esses senos máximos e mínimos, logo:

Ou seja:

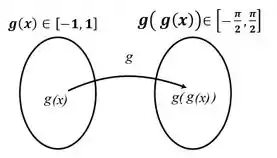
Ao juntarmos a primeira e a segunda imagem pra fazer a composta, vemos que tem duas definições:

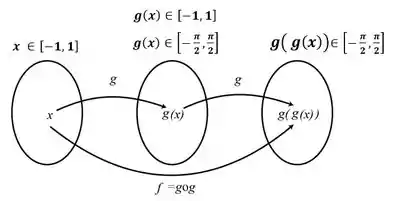
Opa, então precisa fazer parte dos dois intervalos ao mesmo tempo? Isso mesmo galera! E a única forma disso ser possível, já que , é se: