Enfocando conceitos
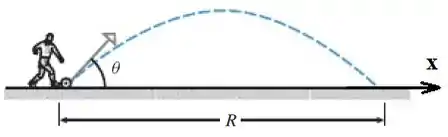
Um jogador de futebol chuta uma bola com uma velocidade inicial de e um ângulo com o plano horizontal (ver figura abaixo). A bola cai no chão a uma distância de depois do chute. Se a resistência do ar for desprezada, então a bola terá uma trajetória parabólica e o alcance horizontal será dado por:
Onde é a velocidade inicial da bola e é a aceleração da gravidade. Usando , aproxime dois valores de , até o grau mais próximo, segundo os quais a bola poderia ter sido chutada. Qual ângulo resultaria em um tempo menor de permanência no ar? Por quê?
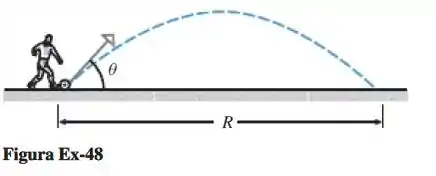
Passo 1
Fala povo! Ó, essa questão deu muito blablabla no início hahaha. Que tal resumir ela? Temos uma imagem, uma fórmula e os comandos da questão:
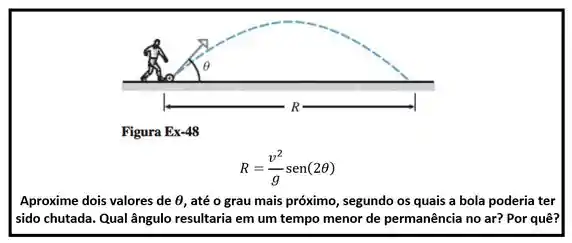
Bem, já que a questão quer saber ângulos, porque não isolarmos esse ? Bora lá:
Sendo, do enunciado:
A fórmula fica:
Pra achar esse resultado, podemos usar a calculadora, um recurso gráfico ou mesmo uma ferramenta de planilhas. Aqui eu vou escolher o último, mas fica a seu critério, ok? Usando a função “=ASEN()” e a função “=GRAUS()” consigo montar a seguinte tabela:
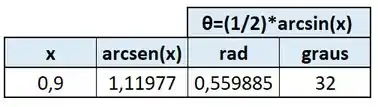
Portanto um valor de que gera esse alcance é . Agora, se olharmos bem para o círculo trigonométrico:
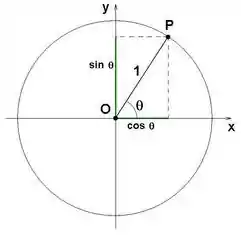
Vemos que nenhum outro ângulo no primeiro quadrante produz o mesmo seno de valor . Porém, pela simetria da mesma imagem, vemos que o ângulo , no segundo quadrante, possui sim o mesmo valor de seno!
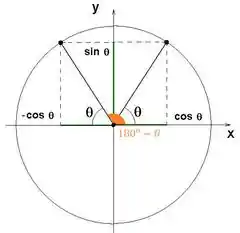
Portanto outro ângulo possível pro chute dessa bola, que gere um alcance de , seria:
Um detalhe importantíssimo aqui no entanto é que chutar a bola a é exatamente a mesma coisa que chutar a só que pra trás.
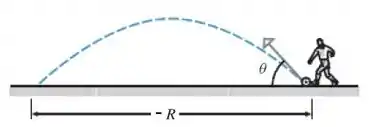
Então, seja:
Teremos:
Resumo da obra:
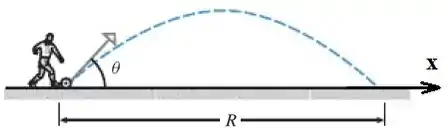
Considerando que o eixo positivo é da esquerda pra direita e que a abertura do ângulo de chute acontece no sentido anti-horário, a bola terá um alcance absoluto de se chutada a ou a .
Passo 2
Po galera, agora queremos saber de permanência no ar: qual ângulo geraria menor permanência? Bem, saca só, como estamos no planeta terra, a bola quando é chutada, está sujeita a aceleração da gravidade. E como toda boa aceleração, temos:
Só que a gravidade só atua no eixo , né não? Então aquela velocidade ali vai precisar ser decomposta. Seja:
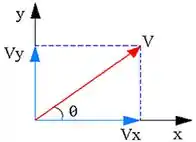
Vamos ter que . Então trocando por e usando só a componente da velocidade, pra subida, temos:
Uma vez que a nossa bola volta ao solo, o valor a ser considerado como tempo total de trajeto é o dobro do tempo de subida! Assim, podemos escrever:
E olha só uma coisa louca: o tempo em função do ângulo é nada mais nada menos que uma função oscilatória. Veja que pra:
Então pra a função seno é uma função estritamente crescente! Dá pra gente notar isso também ao olharmos para o círculo trigonométrico. Oras, se a gente aumenta o tempo total no ar quanto maior o ângulo que aplicamos, o menor tempo possível de permanência no ar vai ser , com tempo nulo. Resumo, se você passar a bola ao invés de isolar ela, ela fica menos tempo no ar hahaha
Resposta
Letra a:
Considerando que o eixo positivo é da esquerda pra direita e que a abertura do ângulo de chute acontece no sentido anti-horário, a bola terá um alcance absoluto de se chutada a ou a .
Letra b:
Seja, pelos cálculos:
Vemos que o tempo de permanência no ar ( é mínimo se ele não for pro ar de início, uma vez que é uma função estritamente crescente no intervalo de chute (no passo , conversamos sobre como ser somente um chute igual a só que da esquerda pra direita).