A Equação de Diferenças Logística. Os problemas de 14 a 19 tratam da equação de diferenças (21) .
- Para , faça o gráfico ou calcule a solução da equação logística (21) para diversas condições iniciais, por exemplo, . Observe que, em cada caso, a solução se aproxima de uma oscilação estacionária entre os mesmos dois valores. Isto ilustra que o comportamento em longo prazo da solução é independente do valor inicial.
- Faça cálculos semelhantes e verifique se a natureza da solução para grande é independente da condição inicial para outros valores de , como .
Passo 1
Nesse exercício, vamos plotar gráficos para cada tipo de condição dada nos itens e fazer uma pequena análise dos mesmos. Para plotar, estarei usando nosso querido python que tanto amamos
Passo 2
- Vamos lá! Basicamente para esse problema vamos apenas plotar cada gráfico como pedido no enunciado. Caso não tenha nenhuma ferramenta para plota-los, sugiro fazer os cálculos em tabelas no excel para facilitar os cálculos.
- Bom, aqui vamos pegar um valor inicial fixo e variar nosso . Assim, temos que:
Para :
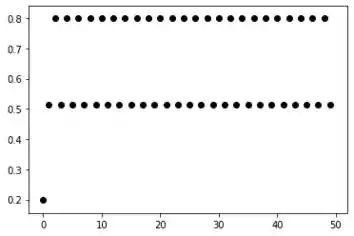
Para :
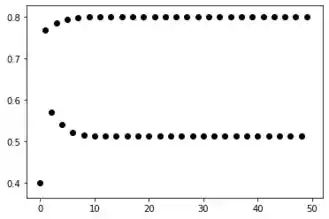
Para :
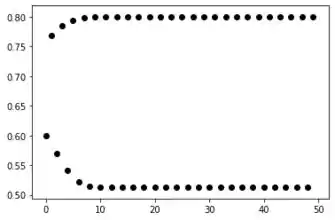
Para :
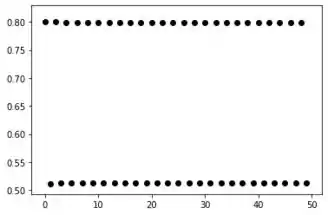
Passo 3
Para e :
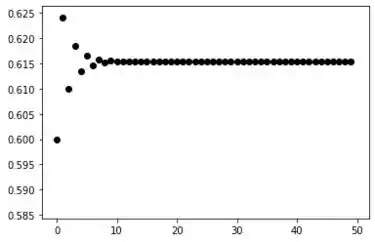
Para e :
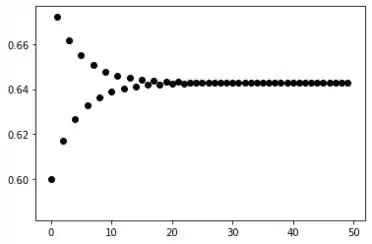
Para e :
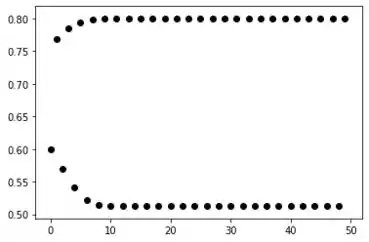
Para e :
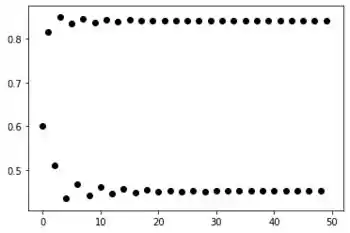
Resposta
Ei, a resposta está no passo a passo :)