Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.9 - Ex. 18
A Equação de Diferenças Logística. Os problemas de 14 a 19 tratam da equação de diferenças (21) .
Calculando ou fazendo o gráfico da solução da Eq. (21) para valores diferentes de , estime o valor de para o qual a solução muda de uma oscilação de período dois para uma de período quatro. De modo análogo, estime o valor de para o qual a solução muda de período quatro para período oito.
Passo 1
Nesse exercício, vamos plotar alguns valores de e analisar para quais valores há uma mudança no período da função observada no gráfico.
Passo 2
Bom, vamos começar olhando os exemplos que temos no capítulo do livro. O próprio livro nos dá quais são os valores de para uma oscilação de período 2 e de período 4. Para a mudança de período 2 para período 4 temos que o necessário é de , e a cara das funções para esses dois períodos é esse
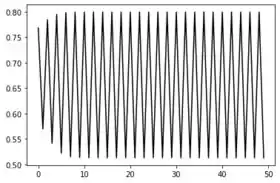
Figura 1: Período 2Figura 2: Período 4
Agora para período 8 temos um certo problema: como dito no próprio capítulo, para qualquer valor a partir de teremos uma solução caótica, então para um período de oscilação 8, teremos que, fazendo uma certa consideração de ainda ser uma solução oscilatória, nosso será de .
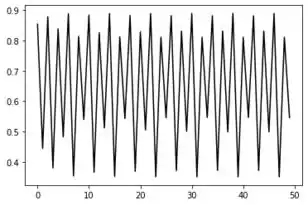
Resposta
Ei, a resposta está no passo a passo :)