A Equação de Diferenças Logística. Os problemas de 14 a 19 tratam da equação de diferenças (21) .
As soluções da Eq. (21) mudam de sequências convergentes para oscilações periódicas de período dois quando o parâmetro passa pelo valor 3. Para ver mais claramente como isto ocorre, efetue os cálculos indicados a seguir.
- Faça o gráfico ou calcule a solução para , respectivamente, usando um valor inicial de sua escolha no intervalo . Estime, em cada caso, quantas iterações são necessária para a solução tornar-se “muito próxima” do valor limite. Use qualquer interpretação conveniente para o significado de “muito próximo” na frase anterior.
- Faça o gráfico ou calcule a solução para , respectivamente, usando a mesma condição inicial que no item (a). Estime, em cada caso, quantas iterações são necessárias para atingir uma solução estado estacionário. Encontre ou estime, também, os dois valores na oscilação estado estacionário.
Passo 1
Nesse exercício, vamos plotar os gráficos utilizando a nossa querida ferramenta de gráficos do python (
Passo 2
- Escolhendo nosso valor de como , teremos que:
Para ;
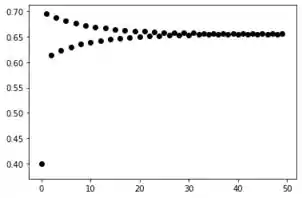
Vemos que para esse valor, já temos mais ou menos as soluções tendendo para um valor limite com a quantidade iterações
Para ;
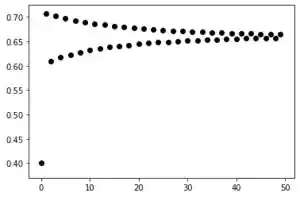
Vemos que para esse valor, já temos mais ou menos as soluções tendendo para um valor limite com a quantidade iterações
Para ;
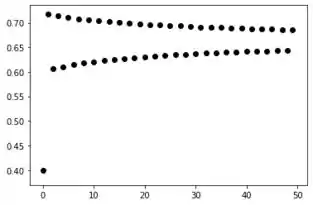
Para esse gráfico precisamos de uma quantidade maior de iterações para chegar no valor limite, com a quantidade de mais ou menos iterações
Passo 3
- Escolhendo nosso valor de como , teremos que:
Para ;

Vemos que para esse valor, já temos mais ou menos as soluções tendendo para um valor limite com a quantidade iterações
Para ;
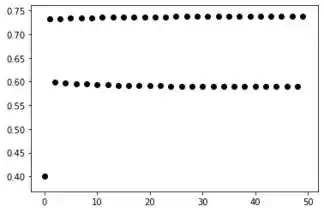
Vemos que para esse valor, já temos mais ou menos as soluções tendendo para um valor limite com a quantidade iterações
Para ;
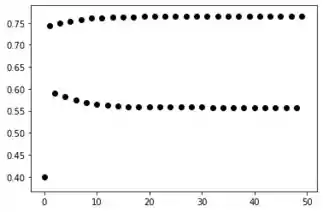
Vemos que para esse valor, já temos mais ou menos as soluções tendendo para um valor limite com a quantidade iterações
Resposta
Ei, a resposta está no passo a passo :)