Nas equações de Lotka-Volterra, a interação entre as duas espécies é modelada por termos proporcionais ao produto das duas populações. Se a população de presas for muito maior do que a de predadores, esse valor poderá ser muito maior do que as interações; por exemplo, um predador pode caçar só quando está com fome, ignorando a presa em outros momentos. Neste problema, vamos considerar um modelo alternativo proposto por Rosenzweig e MacArthur.
(a) Considere o sistema
Determine todos os pontos críticos desse sistema.
(b) Determine o tipo e as propriedades de estabilidade de cada ponto crítico.
(c) Desenhe um campo de direções e um retrato de fase para esse sistema.
Passo 1
Vamos começar relembrando o que é um ponto crítico. Ponto crítico é um ponto do sistema em que as derivadas são nulas. Então, o que vamos fazer é igualar uma das duas derivadas a zero e encontrar os valores que são raízes da equação:
Ou
Vamos agora aplicar estes valores de e que encontramos na outra derivada para definir os pontos críticos. Para :
Ou
Então, nossos primeiros pontos críticos são e . Para :
Então, nosso último ponto crítico é .
Passo 2
Agora que encontramos os pontos críticos, vamos para o item (b). O item (b) pede para determinar o tipo e a estabilidade de cada ponto crítico. Para isso, vamos começar chamando:
Para definir cada ponto vamos aplicar agora a matriz jacobiana. Ela é dada por:
O primeiro ponto crítico é :
Então, e :
Portanto, para o ponto crítico temos , então este ponto é um ponto de sela instável.
Vamos agora para o segundo ponto crítico, :
Então, para este ponto teremos e . Portanto, e, assim, é um ponto de sela instável.
O terceiro ponto crítico é . Aplicando na jacobiana:
Então, temos uma raiz da forma , então o ponto é um nó assintoticamente estável.
Passo 3
Para o item (c) devemos agora desenhar o campo de direções e o retrato de fase do sistema. O primeiro passo será obter a derivada . Sabemos que:
Se fizermos :
Então:
Aplicando a derivada para diferentes pontos do plano , seremos capazes de obter o campo de direções do sistema. Usando o Excel devemos chegar em algo parecido com:

Para obter o retrato de fases devemos observar a tendência do campo. Ao fazer isso obtemos:
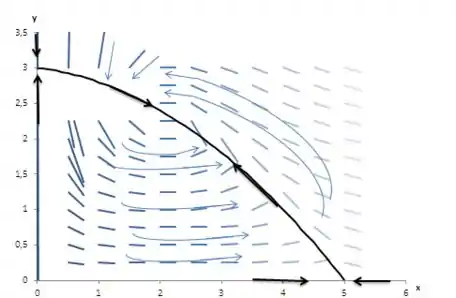
Resposta
Pontos críticos:
ponto de sela instável;
ponto de sela instável.
nó assintoticamente estável.