Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 55
O que está errado na equação?
Passo 1
Fala galera, nessa questão temos a seguinte integral:
E o enunciado nos diz que o resultado dela é:
E nos pergunta o que há de errado.
Primeiro, temos que saber que para a função ser integrável ela precisa ser contínua no intervalo de integração.
Nossa função é:
Essa função é descontínua em e faz parte do intervalo de integração!
Passo 2
Se esboçarmos o gráfico de , ficamos com o gráfico de uma função com par. Que é basicamente um “vulcão” centrado no ponto .
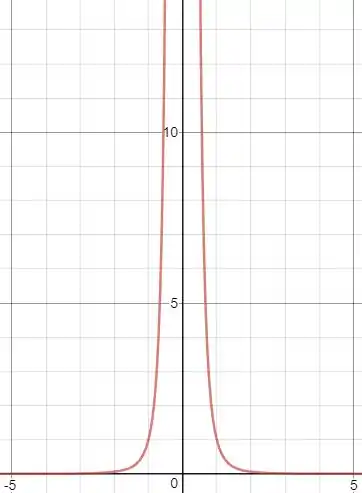
Pelo gráfico, conseguimos ver que há uma descontinuidade na função no ponto , então, podemos concluir que não é contínua no intervalo .
Como ela não é contínua nesse intervalo, a parte 2 do Teorema Fundamental do Cálculo não pode ser aplicado, então esta integral não existe.