Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 23

Encontre os pontos sobre a elipse que estão mais distantes do ponto

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar os pontos sobre a elipse que estão mais distantes do ponto .

Então, vamos começar desenhando a elipse pra entender o que ele tá dizendo:

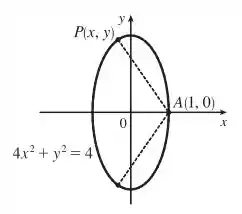
Observe o ponto está contido na elipse e nós queremos encontrar um ponto que esteja o mais longe possível do ponto . Isso quer dizer que queremos que a distância de um ponto a outro seja máxima. Mas como vamos calcular a distância entre esses pontos?

Vamos usar a fórmula da distância entre dois pontos:

Pra facilitar nas contas, a gente considera que seja uma distância ao quadrado, que vamos chamar de , e teremos:

Então, nós vamos maximizar essa função. Mas pra isso, vamos precisar colocar ela em função de uma única variável. Pra isso, vamos usar a equação da elipse, isolando e substituindo na fórmula da distância. Depois, derivamos a equação para encontrar os pontos críticos e avaliamos o ponto de máximo.

Vamos lá!

Passo 2

Podemos ver que há dois pontos mais distantes do ponto . A distância entre um ponto qualquer para o ponto é dada por:

Mas, como estamos trabalhando o quadrado da distância, teremos:

Se pegarmos a equação da elipse e isolarmos ficamos com:

Então, substituindo em , temos:

Passo 3

Agora vamos encontrar a distância máxima. Pra isso, precisamos encontrar os pontos críticos dessa função. Então, vamos começar derivando ela:

Agora igualando a zero, vamos ter:

E isolando :

Como é uma parábola de concavidade voltada para baixo, e função apresenta apenas um ponto crítico, podemos dizer que esse ponto é um ponto de máximo. Então, vamos descobrir o valor de no ponto, substituindo na equação da elipse: