Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 56
O que está errado com a equação?
Passo 1
Oie, tudo certo 😊?
Essa questão nos dá uma integral junto da sua solução, ou seja,
e nos questiona o que há de errado nisso.
Sendo assim, precisamos usar os nossos conhecimentos em cálculo para entender o motivo disso não estar certo, beleza?
Mas, olhando para as igualdades dadas, percebemos que a Parte do Teorema Fundamental do Cálculo foi utilizada para resolver a integral
cujo intervalo de integração é e o integrando é a função
🤔 Mas o que esse Teorema diz mesmo?
Bem, ele diz que se quisermos calcular a integral definida de uma função contínua em um intervalo é suficiente calcular a diferença dos valores de uma primitiva nos extremos do intervalo.
Em termos matemáticos, a parte 2 do Teorema Fundamental do Cálculo diz o seguinte:
onde é uma função contínua no intervalo e é uma primitiva de .
Dessa forma, vamos analisar o que está acontecendo com a função no intervalo de integração, beleza? E o que pode estar dando errado.
Bora lá!! 😉
Passo 2
Utilizando uma ferramenta gráfica para esboçar o gráfico da função
obtemos o gráfico abaixo.
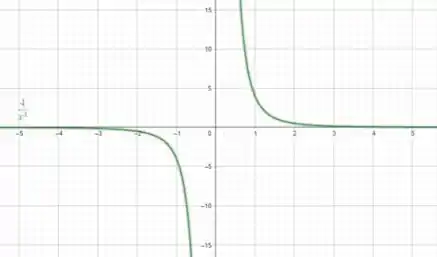
Pelo gráfico, conseguimos ver que há uma descontinuidade na função no ponto , certo?
Como a função não é contínua no intervalo , então não podemos usar a Parte do Teorema Fundamental para calcular a integral
pois a continuidade é uma condição muito importante para que a integral seja dada por
com sendo uma primitiva de .
Resposta
Portanto, o erro na equação original está no fato de utilizar a Parte do Teorema Fundamental do Cálculo para o cálculo da integral
pois a função
tem uma descontinuidade em e para usarmos o Teorema, deve ser contínua em todo o intervalo de integração.