Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 57
O que está errado na equação?
Passo 1
Galera... nessa questão nos é dada a seguinte integral:
E o enunciado diz que o resultado é:
E nos pergunta qual é o erro dessa resposta.
Bom, primeiro, para uma função ser integrável é necessário que ela seja contínua no intervalo de integração.
Passo 2
A função é dada como:
No intervalo que vai de até , temos que no ponto do intervalo o cosseno vale zero e portanto essa função possui uma descontinuidade, afinal não podemos dividir por zero.
Se esboçarmos o gráfico de , ficamos com
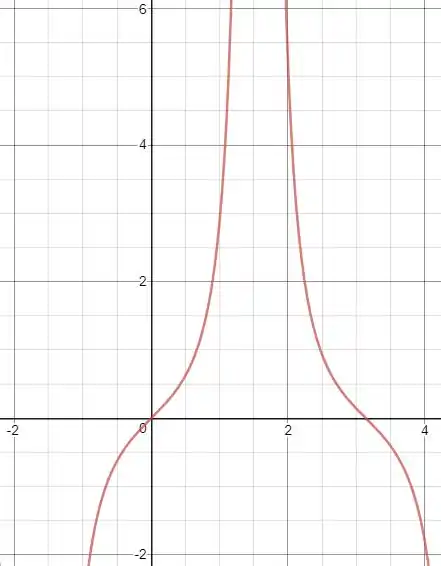
Pelo gráfico, conseguimos ver que há uma descontinuidade na função no ponto , pois
, então, podemos concluir que não é contínua no intervalo .
Como ela não é contínua nesse intervalo, a parte 2 do Teorema Fundamental do Cálculo não pode ser aplicado, então esta integral não existe.