Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 15d
Esboçar o gráfico da curva descrita por um ponto móvel , quando o parâmetro varia no intervalo dado. Determinar a equação cartesiana da curva em cada um dos itens:
d)
Passo 1
Então pessoal, a estratégia para determinarmos a equação cartesiana da curva será isolarmos em uma das funções e substituir na outra função, porque aí teremos uma equação em termos de e , que é exatamente o que queremos, tudo bem? Tendo isso em vista, temos que:
Substituindo na segunda equação, teremos:
E essa é a nossa equação cartesiana.
Passo 2
Da equação que encontramos, fica bem tranquilo de observar que se trata de uma equação do segundo grau, não é mesmo? Sendo assim, o gráfico associado é uma parábola no plano . Se esboçarmos o gráfico dessa função, teremos:
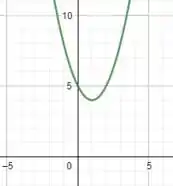
Aqui vale ressaltar que o gráfico foi plotado em 2D, então basta imaginar essa parábola com uma elevação em .
E está aí nossa resposta, galera! 😊
Resposta
