Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 15b

Esboçar o gráfico da curva descrita por um ponto móvel P x ,   y , quando o parâmetro t varia no intervalo dado. Determinar a equação cartesiana da curva em cada um dos itens:

b) x = 4 . cos ⁡ t ,   y = 4 . s e n   t ,   z = 2   0 ≤ t ≤ 2 π

Passo 1

Então pessoal, a estratégia que vamos utilizar para determinar a equação cartesiana da curva será: como x e y estão escritos em termos de seno e cosseno, vamos utilizar a relação fundamental da trigonometria para escrever tudo em uma expressão só, tudo bem? A relação é:

s e n 2 x + c o s 2 x = 1

Sabendo disso, então bora pra cima agora!

Passo 2

Se elevarmos x ao quadrado, teremos:

x 2 = 16 . c o s 2 t

c o s 2 t = x 2 16

Se elevarmos y ao quadrado, teremos:

y 2 = 16 . s e n 2 t

s e n 2 t = y 2 16

Se elevarmos x ao quadrado, teremos:

x 2 16 + y 2 16 = 1

x 2 + y 2 = 16

E essa é a nossa equação cartesiana.

Passo 3

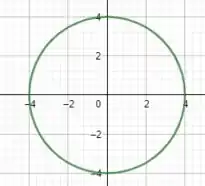
Da equação que encontramos, temos que se trata de uma parábola de raio 4 no plano de z = 2 . Se esboçarmos o gráfico em 2D, teremos:

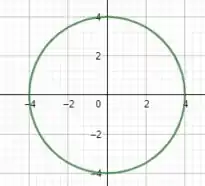
E está aí nossa resposta, galera! 😊

Resposta

x 2 + y 2 = 16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o centro e o raio das seguintes circunferências e depois escrever uma equação vetorial para cada uma.a) x 2 + y 2 - 2 x + 5 y - 3 = 0
Obter a equação cartesiana das seguintes curvas:c) r → s = s 2 - 1 ,s 2 + 1 ,2
Esboçar o gráfico da curva descrita por um ponto móvel P x ,y , quando o parâmetro t varia no intervalo dado. Determinar a equação cartesiana da curva em cada um dos itens:a) x = 2 . cos ⁡ t ,y = 2 .
Obter a equação cartesiana das seguintes curvas:a) r → t = t 2 ,3 t + 5
Esboçar o gráfico da curva descrita por um ponto móvel P x ,y , quando o parâmetro t varia no intervalo dado. Determinar a equação cartesiana da curva em cada um dos itens:c) x = 2 + 4 . s e nt ,y = 3