Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 5

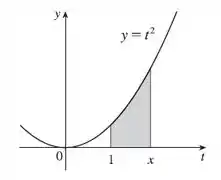
Esboce a área representada por g x . A seguir, encontre g ' x de duas maneiras: (a) utilizando a Parte 1 do Teorema Fundamental e (b) calculando a integral usando a Parte 2 e então derivando.

g x = ∫ 1 x t 2 d t

Passo 1

O gráfico da área representada por g x é a parte abaixo da função y = t 2 entre t = 1 e t = x :

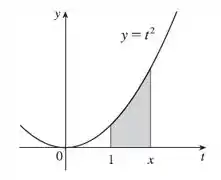
Passo 2

  1. Vamos achar g ' x pela Parte 1 do Teorema Fundamental que nos diz que:

    2. g x = ∫ a x f t d t             a ≤ x ≤ b

    é contínua em a , b e derivável em a , b e g ' x = f x .

    Assim temos que a = 1 e assim:

    g ' x = f x = x 2

    Passo 3

  2. Pela Parte 2 vamos calcular a integral:

∫ 1 x t 2 d t

Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.

É simples achar as primitivas da função, vamos usar uma expressão da Tabela de Integrais Indefinidas:

∫ x n d x = x n + 1 n + 1 + C   n ≠ - 1

Assim:

∫ t 2 d t = t 2 + 1 2 + 1 + C = t 3 3 + C

Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:

∫ a b f x d x = F b - F a

Assim ficamos com:

∫ 1 x t 2 d t = t 3 3 1 x = x 3 3 - 1 3 3 = x 3 3 - 1 3

Achando a derivada agora:

g ' x = x 3 3 - 1 3 ' = 3 x 3 - 1 3 - 0 = x 2

Resposta

  1. g ' x = x 2
  2. g ' x = x 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As superfícies planas mostradas estão imersas verticalmente em água. Encontre a força do fluido sobre cada superfície.
As superfícies planas mostradas estão imersas verticalmente em água. Encontre a força do fluido sobre cada superfície.
Suponha que uma superfície plana esteja imersa verticalmente em um fluido de peso específico ρ . Dobrando-se ρ , dobra também a força sobre a superfície? Explique seu raciocínio.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A pressão e a força têm as mesmas unidades no sistema M K S .
Em qualquer tanque d’água com uma base plana, a força do fluido na base do tanque é, no máximo, igual ao peso da água no tanque, independentemente do formato do tanque.