Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 2
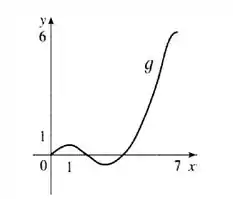
Seja onde é a função cujo gráfico é mostrado.
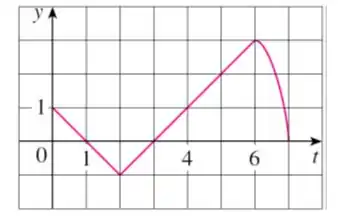
(a) Calcule para .
(b) Estime .
(c) Onde tem um valor máximo? Onde possui um valor mínimo?
(d) Faça um esboço do gráfico de .
Passo 1
Item a:
Se , então:
Para , temos:
0
Para , temos:
Para , temos:
Se a curva é negativa em certo intervalo, a integral é negativa.
Para , temos:
Para , temos:
Para , temos:
Para , temos:
Passo 2
Item b:
Para temos:
Devemos estimar então, a área do gráfico entre e :
Podemos ver que a área da integral é maior que o triangulo de base e altura bem como é menor que o retângulo de mesma base e mesma altura, logo:
Podemos estimar então, como a média do intervalo:
Então: o valor estimado de é
Passo 3
Item c:
Pelos valores calculados em (a) e (b), podemos ver que tem máximo em e mínimo em .
Passo 4
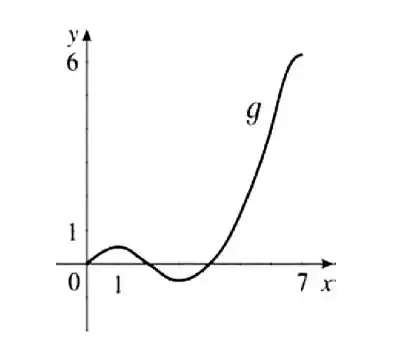
Item d:
O gráfico de é esboçado por:
Resposta
(a) 0, , , , , , .
(b)
(c) tem máximo em e mínimo em .
(d)
