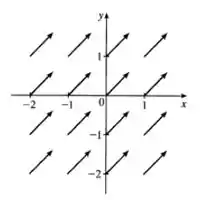
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .
Passo 1
Oi galera, tudo bem? Precisamos fazer o campo vetorial, né?
Bom, esse vetor tem essa cara aqui, né?
Olha só, ele tem componentes iguais de módulo … Bom, pra fazer o campo vetorial a gente precisa saber o tamanho desse vetor, beleza?
Vamos achar o tamanho desse vetor fazendo o módulo dele, olha só:
Show!
Passo 2
Agora que temos o tamanho do vetor, precisamos saber para onde o campo vetorial vai apontar… Bom, como as componentes são iguais em sinal e em módulo, eles são paralelos à reta, ou seja, temos !
Se a gente colocar isso num gráfico, podemos representar assim:
Prontinho! Conseguimos!
Resposta