Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 34
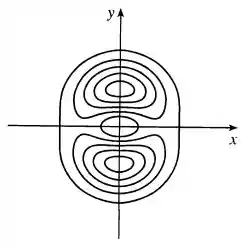
Faça um esboço do diagrama de contorno da função cujo gráfico é mostrado.
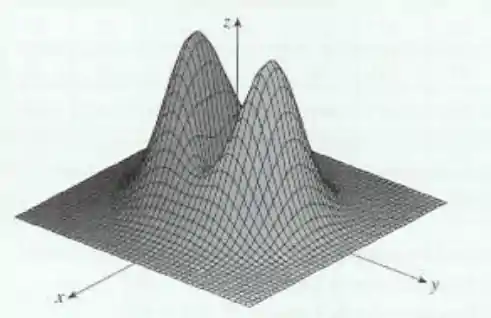
Passo 1
Olá, meu brother. Vamos resolver essa atividade aqui.
A gente tem o gráfico de uma função qualquer:
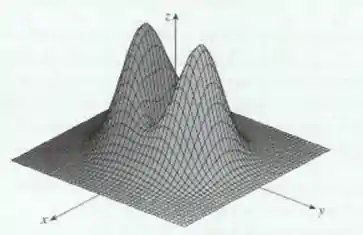
E a gente precisa encontrar o diagrama de contorno dela. A questão aqui não é fazer o diagrama, mas o que seria esse tal de diagrama de contorno, sabendo o que ele é, fica mais fácil você conseguir criar o diagrama de contorno para qualquer gráfico.
Um diagrama de contorno, também conhecido como mapa de contorno ou gráfico de contorno, é uma representação gráfica de uma função de duas variáveis . Ele mostra curvas de nível, que são linhas que conectam pontos com o mesmo valor de . Estas curvas ajudam a visualizar a forma e a variação da função em uma superfície bidimensional.
Passo 2
Galera, aqui só temos que fazer contornos em volta desses “montes”, lembrando que pontos que parecem ter a mesma altura pertencem à mesma linha de contorno:
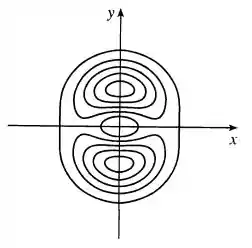
Então basicamente o que temos é uma planificação do gráfico tridimensional, fazemos isso e visualizamos de cima.
Resposta
