Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.7 - Ex. 56
Esboce os círculos nos Exercícios 53-56. Dê coordenadas polares para seus centros e identifique seus raios.
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
Neste problema, nosso objetivo usar as relações a seguir para transformar os círculos de coordenadas polares para coordenadas cartesianas.
Em seguida, a partir da equação cartesiana, obter o centro e o raio e convertê-los para coordenadas polares. Ah, e não podemos esquecer de esboçar o gráfico.
Simbora?
Passo 2
Vamos começar multiplicando ambos os lados da equação por r:
Usando as relações citadas no passo 1, temos:
Vamos usar o método de completar quadrados somando 16 em ambos os lados da igualdade, assim:
Usando a fatoração do produto notável, temos:
Uma vez que a equação geral de uma circunferência é dada por:
Onde são as coordenadas do centro e o seu raio.
Temos então:
Centro: e Raio:
Passo 3
Porém estas coordenadas não estão no formato polar, vamos convertê-las.
Sendo , temos que:
Para , então:
Logo, seu raio é e o centro
Por fim, seu gráfico terá o seguinte formato:
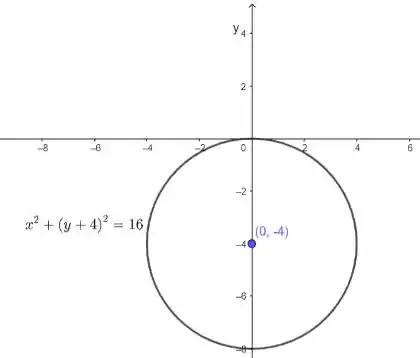
Espero ter ajudado! Abraços e até a próxima!
Resposta
Raio: . Centro: .