Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 29
Esboce a curva com a equação dada.
Passo 1
Fala ai galera. Você sabe o que esta equação representa?
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Como nessa equação o não aparece, ele varia livremente, enquando o aparece como uma constante, ou seja, todos os pontos estarão à uma mesma angulação do eixo .
Passo 2
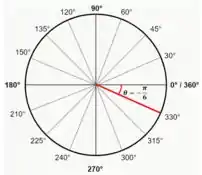
Quando temos uma equação onde o é constante, será sempre uma reta com ângulo em relação ao eixo igual a e ela sempre parte da origem pro infinito, não tem uma parte “negativa” desta reta.
Como é negativo, a reta será abaixo do eixo com angulação igual ao módulo de .
Sendo assim, o ângulo , corresponde a . Isso indica que estamos indo a graus no sentido horário a partir do eixo positivo.
Passo 3
Para a construção da curva, vamos esboçar uma curva que representa , você está desenhando uma linha reta que se estende na direção (ou se considerarmos a rotação completa) a partir do eixo x positivo no sistema de coordenadas polares.
Ficanda da seguinte forma.
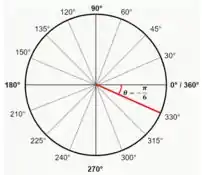
Resposta
