Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 16
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Olá, meu querido amigo. A gente precisa realizar duas coisas nessa atividade. Precisamos eliminar o parâmetro da curva parametrizada:
E consequentemente passar essa equação para as coordenadas cartesianas. E iremos fazer isso isolando o em uma equação e substituindo ele na outra equação.
Precisamos também encontrar o gráfico da curva. A gente pode fazer isso com uma tabela, com valores de e respectivos valores para e . Depois a gente vai utilizar o GeoGebra para plotar o gráfico.
Passo 2
Podemos isolar o parâmetro na equação do fazendo:
Elevando ambos os lados a base :
Utilizando a propriedade de logaritmos:
Substituindo na equação do :
E, como
E
Então
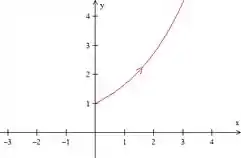
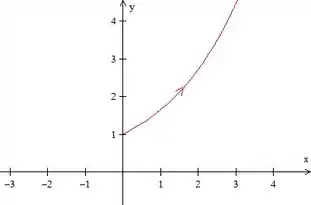
Assim, nossa curva começa no ponto e depois vai crescendo indefinidamente.
Passo 3
Criando a tabela:
Traçando nossa curva, temos:
Resposta
