Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 46
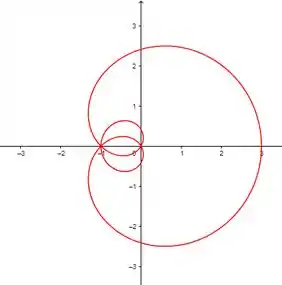
Esboce a curva com a equação dada.
Passo 1
O que a equação representa?
Nas equações polares o representa a distancia do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido, então vamos na raça.
Assim, vamos dar uma analisada no comportamento da função substituindo valores até que completemos uma volta, certinho?
Passo 2
Primeiramente vamos calcular valores de para alguns valores de :
Vamos calcular para e . (Com esses valores a gente consegue descrever o comportamento da curva como um todo).
Passo 3
Agora vamos fazer para os outro ângulos em sentido anti-horário:
Aqui o tinha saído de e parou em no primeiro quadrante.
Passo 4
Agora para o segundo quadrante, chegando em :
Aqui o tinha saído de e parou em no final do segundo quadrante.
Passo 5
Agora para o terceiro quadrante, chegando em :
Aqui o tinha saído de e parou em no terceiro quadrante.
Passo 6
Agora para o quarto quadrante, chegando em :
Aqui o tinha saído de e parou em no quarto quadrante.
Passo 7
Com isso, ao esboçarmos a nossa função, o nosso gráfico terá a seguinte configuração:
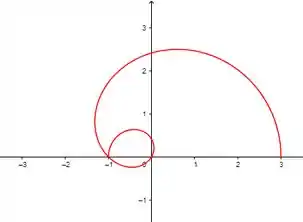
Note que o gráfico não finalizou de onde partimos.
Assim, se fizermos outro ciclo, obteremos a seguinte forma:
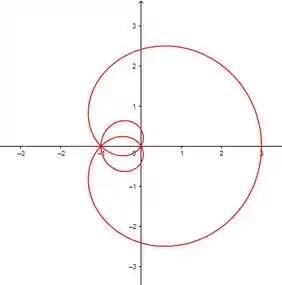
Resposta
