- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Fala ai galerinha! De boa?
Nessa questão precisamos determinar a equação cartesiana de uma curva parametrizada pelas seguintes equações, e . Além disso, deseja-se esboçar a curva no plano cartesiano e indicar a direção na qual a curva é traçada à medida que o parâmetro varia.
E o que podemos fazer para resolver?
- Identificar as equações paramétricas.
- Eliminar o parâmetro.
- Esboçar a curva e verificar a direção da curva.
Vamos começar!
Passo 2
a) Se observarmos com carinho, vamos perceber que esse expoente negativo aí no tá queremos nos enganar mas não vai conseguir, porque
Ou seja, considerando , temos
E como não há nenhuma restrição para o parâmetro, estamos falando da curva inteira.
Só precisamos tomar cuidado que esse aí no numerador tem que ser sempre maior que zero, assim
Passo 3
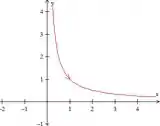
Para a construção da curva. Podemos concluir que :
- A equação representa uma hipérbiole nos quadrantes e
- Para , e
- Para , e
- Quando aumenta, aumenta e diminui, seguindo uma direção específica nos quadrantes.
Obtemos o seguinte gráfico
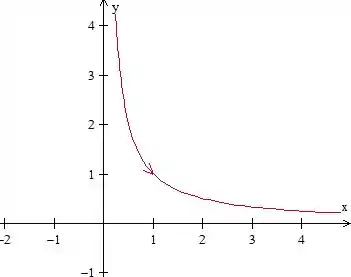
Resposta