Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 30
Esboce a curva com a equação dada.
Passo 1
Fala ai pessoal! Tudo trânquilo?
Para esboçar a curva representada pela equação em coordenadas polares, precisamos primeiro resolver essa equação para encontrar os valores de correspondentes. Ou seja, a partir dos valores encontrados de saberemos a cara da curva.
Agora sim. Você está preparado para resolver.
Vamos lá!
Passo 2
Vamos entender um pouco sobre a equação dada.
Nas equações polares o representa a distancia do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Já que se trata de uma equação quadrática é esperado que assuma dois valores, então nosso gráfico terá provavelmente duas circunferências.
Para isso, vamos calcular os valores de usando nosso querido Bhaskara
Primeiramente calculando o
Sendo , e
Passo 3
Agora para achar os valores de , substituímos o , na equação do r
Pegando temos o valor
Pegando temos
Passo 4
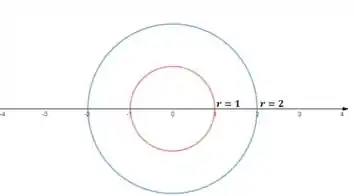
Temos então dois valores de e o variando livremente, o que nos leva à duas circunferências com raios iguais e , centralizados na origem.
No plano:
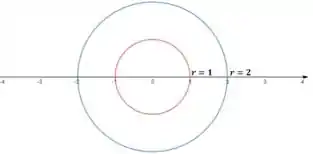
Resposta
