Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.2 - Ex. 4

(a) Esboce o gráfico da curva plana com equação vetorial dada.

(b) Determine r’(t).

(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.

r t = 1 + t ,   √ t ,                                     t = 1

Passo 1

Eai. De boa?

Bora iniciar mais uma questãozinha! Primeiro que tal pensarmos sobre como resolver-la?

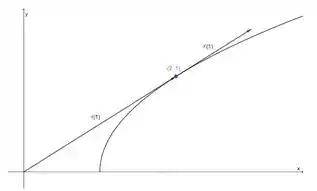
Para resolver a questão, primeiro esboçamos a curva desenhando alguns pontos chave baseados na equação vetorial r ( t ) = ( 1 + t , t ) . Em seguida, encontramos a derivada r ' ( t ) para obter a direção do vetor tangente. Por fim, no ponto dado t = 1 , desenhamos o vetor posição r ( 1 ) e o vetor tangente r ' ( 1 ) para visualizar a curva e sua direção naquele ponto.

E agora, partiu resolver?

Passo 2

Na letra A, as equações paramétricas correspondentes à função vetorial dada são:

x = 1 + t                                               y = t

Isolando-se t em ambas, obtemos

t = x - 1                                                 t = y 2

Com base nos valores do parâmetro obtidos acima, temos

x = y 2 + 1

Esta equação é uma outra representação da função vetorial r ( t ) . Como ela já tem forma mais conhecida é mais fácil representá-la.

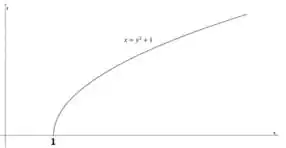
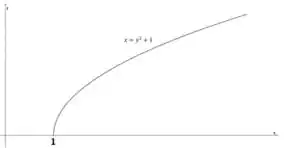
A curva representada por x = y ² + 1 é uma parábola que se abre para a direita. Isso significa que a curva se estende horizontalmente ao longo do eixo x e é limitada na direção vertical ao longo do eixo y . Além disso, O ponto de início da parábola está localizado em ( 1,0 ) porque quando y = 0 , temos x = 0.2 + 1 = 1 . Portanto, a parábola passa pelo ponto ( 1,0 ) e se estende para a direita.

Passo 3

Na letra b, iremos determinar a função r ' ( t ) derivando as componentes de r ( t ) .

r t = 1 + t ,   t

r ' t = d d t 1 + t ,   t

r ' t = ( 1 , 1 2 t )

Passo 4

O vetor posição r ( t ) em t = 1 é

r 1 = ( 2 ,   1 )

Por outro lado, o vetor tangente em t = - 1 , tem origem no ponto ( 2 ,   1 ) e é dado por

r ' 1 = 1 , 1 2

Com base nos resultados obtidos podemos representar esses vetores conforme mostrado na figura abaixo.

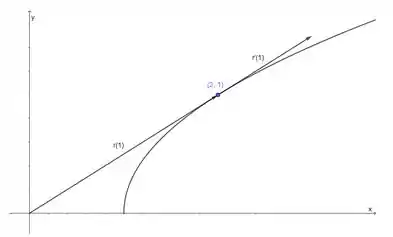
Resposta

  2. r ' t = ( 1 , 1 2 t )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 7 representar graficamente os seguintes campos vetoriais. f → x , y = x , y 2
O campo f → x , y = y i → - x j → representa a velocidade de um volante em rotação rígida em torno do eixo z. Descrever graficamente o campo. Qual o sentido do movimento de rotação?
As funções a seguir definem campos vetoriais sobre R 2 . Determinar e fazer os gráficos das curvas onde | f → | é constante. f → x , y = x i → + y j → .
Escrever uma função vetorial em três dimensões que define um campo vetorial, cuja intensidade seja igual a 1.
As funções a seguir definem campos vetoriais sobre R 2 . Determinar e fazer os gráficos das curvas onde | f → | é constante.c) f → x , y = 2 i → + x j → .