Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 10.5 - Ex. 13
Encontre os vértices e os focos da elipse e esboce o seu gráfico.
Passo 1
Nessa questão, nos foi dada a equação de uma elipse, para encontrarmos seus vértices e focos. A equação que temos em mão é a seguinte:
Mas tem alguma coisa diferente nessa elipse, a equação não está do jeito que estamos acostumados a trabalhar, vamos ajeitar ela para ficar com a cara
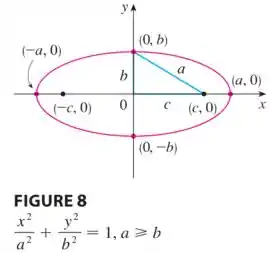
Esse será o nosso segundo passo. Mas saiba que para equações de elipse desse tipo, os seus focos estão em:
Onde:
E os vértices estão em:
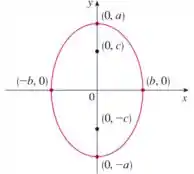
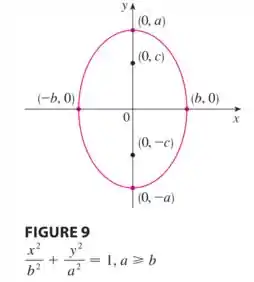
Já para elipses da forma:
Temos algumas mudanças, os focos ficam em:
E os vértices ficam em:
Os gráficos também mudam, temos o seguinte:
Passo 2
Agora está na hora de colocarmos na forma que conhecemos uma elipse.
Repare que do lado direito temos um , então vamos dividir a equação toda por para ver como fica:
Observe que como não temos nenhum número somando ou subtraindo do e do podemos dizer que a elipse é centrada na origem.
A equação geral de uma elipse centrada na origem é , e quando temos o número maior embaixo do esta é uma elipse com eixo maior no eixo .
O foco de uma elipse desse tipo é dado por
Como nossa equação é
temos que
Os vértices de uma elipse centradas na origem são:
Então,
Passo 3
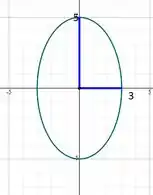
Vamos esboçar essa elipse seguindo o gráfico de ajuda:
