Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 39
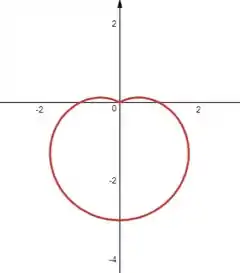
Esboce a curva com a equação dada.
Passo 1
Opa, tudo bem? Bom... o enunciado nos deu a seguinte equação polar:
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Queremos esboçar esse gráfico.
Então como faremos isso???
Bom... Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido...
Então vamos colocar alguns valores para e substituir na equação a fim de analisarmos o seu comportamento!! 😉
Passo 2
Primeiramente calculamos valores de para alguns valores de :
Vamos calcular para :
Para :
Para :
Para :
Para :
Passo 3
Para fazer a análise desses valores, vamos precisar analisar o círculo trigonométrico para a função seno com seus valores:
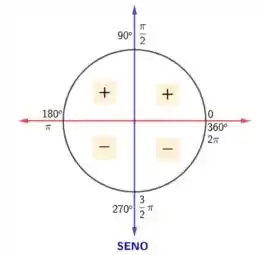
Assim, podemos observar que:
- No primeiro quadrante o varia de a e a função varia de a ;
- No segundo quadrante o varia de a e a função varia de - a ;
- No terceiro quadrante o varia de a e a função varia de a ;
- E no quarto quadrante o varia de a e a função varia de a .
Se nós considerarmos os valores negativos da função como uma distância no sentido oposto, teremos o seguinte gráfico:
Se desconsiderarmos todos os valores negativos da função, teremos o seguinte gráfico:
Resposta
