Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 70
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.
70. (curva valentina)
Passo 1
Falaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar:
Utilizando um software matemárico, queremos plotar essa curva e escolhermos um parâmetro para termos certeza que plotaremos ela inteira.
Nesse sentido, a gente vai plotar e analisar um padrão no nosso gráfico.
Com isso, a gente vai determinar o nosso parâmetro!!
Agora bora lá!! 😉
Passo 2
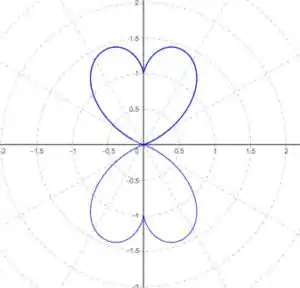
Então pessoal, se plotarmos o gráfico dessa curva polar, teremos o seguinte:
Aqui vale ressaltar que o gráfico continua indefinidamente, tanto para a esquerda quanto para a direita, ok?
E como fazemos para definir o intervalo do parâmetro?
É tranquilo galera, basta olharmos para o gráfico e ver em que ponto ele começa a se repetir!
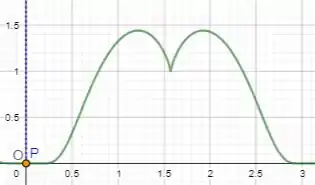
Nesse caso, o gráfico começa em e vai até , a partir disso ele começa a se repetir!
Sendo assim, nosso parâmetro será , veja o plano cartesiano:
Agora, plotando a curva no plano das coordenadas polares, temos esses coraçõezinhos:
Perceba que para plotarmos um coração, a gente utiliza o intervalo , que é o nosso parâmetro!!
Resposta
