Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 10
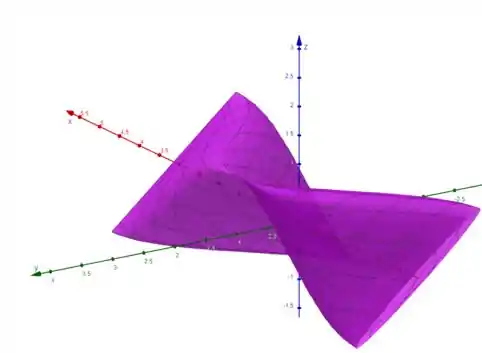
Identifique a superfície que tem a equação paramétrica dada.
,
Passo 1
E aaaiiii galera, beleza!?
Devemos identificar a superfície que tem a equação paramétrica a seguir:
,
Para fazer isso existem vários softwares. Um dos melhores para se plotar gráfico é o Geogebra 3D, pois possui uma linguagem de fácil entendimento e é gratuito.
Assim, não tem muito segredo nessa questão. Você deve entrar com as informações da parametrização no Geogebra 3D e traçar o gráfico.
Bora lá fazer isso!
Passo 2
Da parametrização, temos que
E temos o seguinte intervalo de variação de e :
Entrando com esses dados no Geogebra 3D, vamos ter:
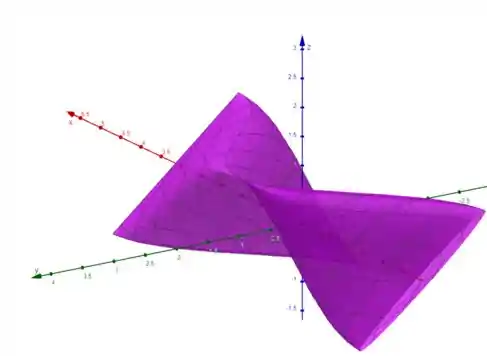
Pessoal, caso queiram plotar, utilizem o seguinte input no Geogebra 3D:
a=Superfície(u,sen(u+v),sen(v),u,-π,π,v,-π,π)
Resposta
Exercícios de Livros Relacionados
Identifique a superfície que tem a equação paramétrica dada. r → u , v = 2 s e nu i → + 3 c o s c o suj → + v k → , 0 ≤ v ≤ 2
Encontre uma parametrização para o hiperboloide x^2 + y^2 - z^2 = 1 .
Considere a superfície parametrizada por φ r , θ = r cos θ ,r sin θ ,θ 0 ≤ r ≤ 10 ≤ θ ≤ 4 π Esboce essa superfície.
Dada a esfera de raio 2 , centrada na origem, encontra a equação do plano tangente a ela no ponto 1,1 ,2 , considerando a esfera como:c) o gráfico de g x , y = 4 - x 2 - y 2 .
Dada a esfera de raio 2 , centrada na origem, encontre a equação do plano tangente a ela no ponto 1,1 , 2 , considerando a esfera como:Uma superfície parametrizada por φ ϕ ,θ = 2 sin ϕ cos θ ,2 si