Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 44
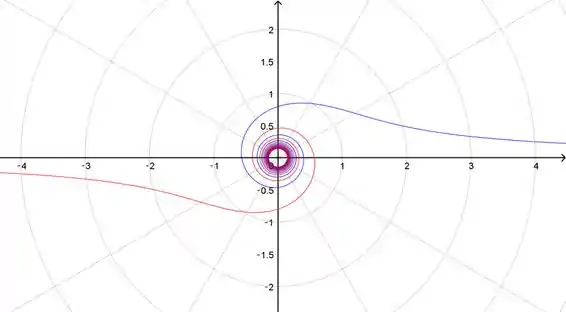
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de em função de nas coordenadas cartesianas
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
Já para encontrarmos o gráfico no eixo polar, nós iremos criar uma tabela com diversos pontos para e seu respectivo valor de .
Passo 2
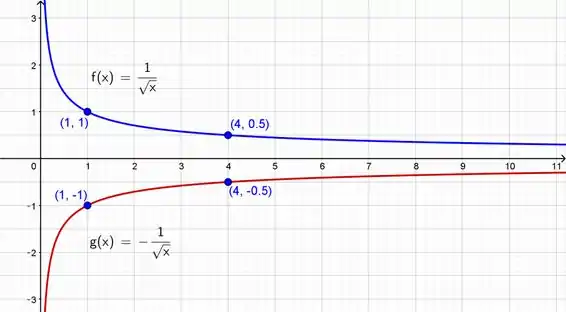
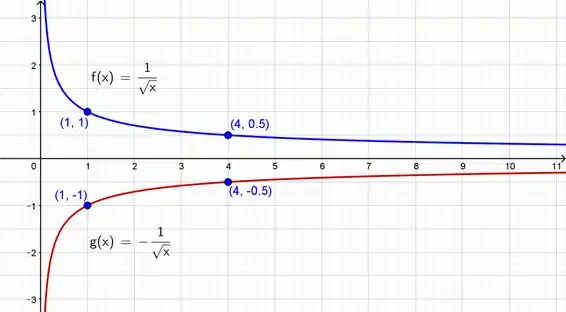
A primeira coisa que vamos fazer é desenhar um plano cartesiano onde o eixo horizontal é o e o vertical o . Da equação podemos ver que .
Para , conforme , o valor de tende ao infinito. Do mesmo modo, , conforme , o valor de tende ao menos infinito.
Passo 3
Nós podemos calcular alguns pontos para ajudar a esboçar o gráfico polar. Usando o incremento de , conseguimos os seguintes valores:
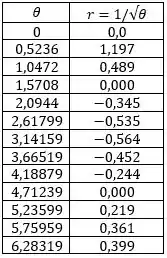
Para valores de próximos a , a curva está distante do polo, depois, conforme aumenta, ela espirala no sentido anti-horário em direção ao polo. O gráfico é desenhado com até aqui, mas continua espiralando para dentro além disso.
A parte da curva onde vem na direção oposta, também espiralando no sentido anti-horário.
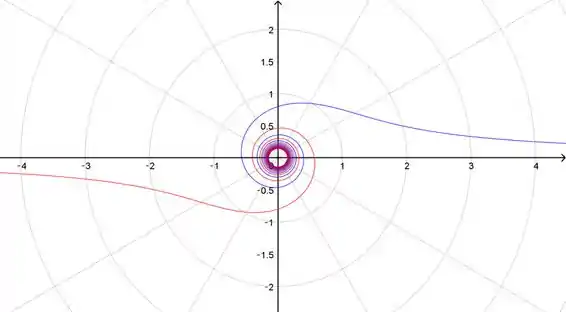
Resposta
