Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 11
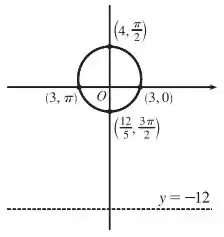
(a) Encontre a excentricidade,
(b) identifique a cônica,
(c) dê uma equação da diretriz e
(d) esboce a cônica
Passo 1
Eaee, belezinha?? Bom... a questão nos dá a seguinte equação:
Primeiramente queremos encontrar a sua excentricidade . (Lembre-se que a excentricidade serve para nos dizer o quão "alongada" ou "achatada" é a forma da cônica.).
Para isso, vamos comparar a nossa equação com a seguinte equação geral:
Onde é a diretriz.
Com o valor da excentricidade, iremos identificar a cônica, onde:
- Se , trata-se de uma elipse;
- Se , trata-se de uma parábola;
- Se , trata-se de uma hipérbole.
Com a curva identificada, poderemos analisar e mostrar a equação da diretriz .
Por fim, iremos plotar a nossa curva. Agora bora lá!! 😉
Passo 2
(a) Beleza, galera? Pra encontrar a excentricidade, vamos comparar a equação do enunciado com a seguinte equação geral de cônicas:
Pra podermos comparar termo a termo, vamos dar uma ajeitadinha na nossa equação multiplicando o numerador e denominador po :
Agora sim podemos comparar direitinho:
Comparando somente os denominadores, vemos que o termo que acompanha é:
Essa é a nossa excentricidade!!
Passo 3
(b) Pra identificar a cônica, analisamos a excentricidade.
Como , então a cônica é uma elipse.
Passo 4
(c) Agora, como a equação da cônica tem “” , a reta diretriz é da seguinte forma:
Show! Agora só falta descobrir quem é , e isso a gente faz comparando os numeradores:
Substituindo :
Então, a equação da reta diretriz fica assim:
Passo 5
(d) Show! Agora vamos fazer uma esboço da cônica, pra você ver que é mesmo uma elipse.
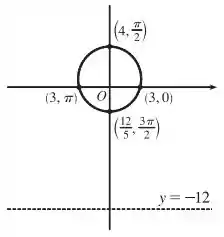
Note que colocamos os pontos onde a elipse faz seus vértices (ela é tão vulgar que parece muito uma circunferência).
A reta pontilhada abaixo é a nossa diretriz 😉
Resposta
(a)
(b) Elipse
(c)
(d)
