Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 19
Trace as cônicas
com e na mesma tela. Como o valor de afeta o formato da curva?
Passo 1
Beleza, galera? Vamos traçar as cônicas que o enunciado pediu e ver o que acontece, ok?
A gente vai utilizar o GeoGebra para traçar essas cônicas. Mas fique a vontade para escolher outro programa gráfico.
A equação geral em forma polar para as cônicas é dada por:
Representando a cônica com excentricidade . O representa a diretriz da nossa cônica.
A gente tem essa equação e iremos substituir os valores de com os que foram dados. Vamos ver o comportamento da nossa cônica parametrizada em função dos valores de . Veja que a diretriz é .
Passo 2
Então ta, vamos gerar o gráfico com o GeoGebra:
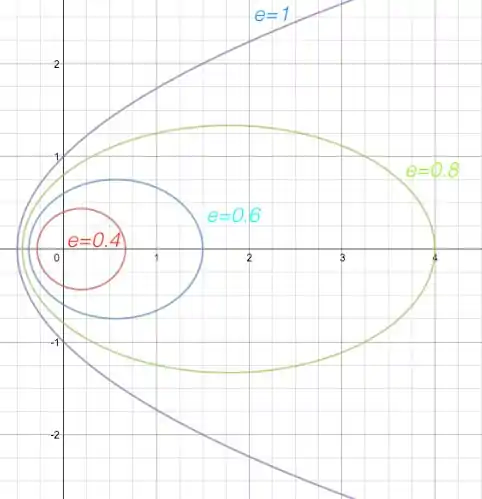
Repare que, quando , a cônica é uma elipse, e à medida que cresce dentro desse intervalo, a elipse vai deixando de ter um formato arredondado e assumindo uma forma mais achatada.
Quando , a cônica é uma parábola.
Resposta
Quanto maior o valor de , mais achatada é a elipse, até chegar em , quando se torna uma parábola.