Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 45

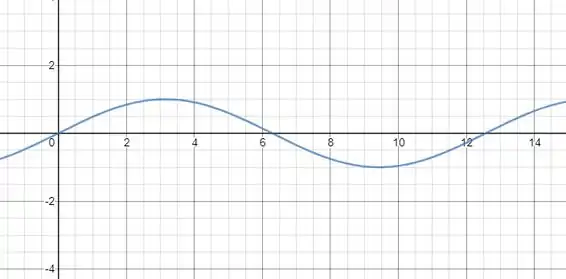
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de em função de nas coordenadas cartesianas

Passo 1

A primeira coisa que vamos fazer é desenhar um plano cartesiano onde o eixo horizontal é o e o vertical o . A amplitude da função é de , logo . Ao multiplicarmos por esticamos o gráfico horizontalmente pelo fator de . Dividindo por , nós obtemos o período:

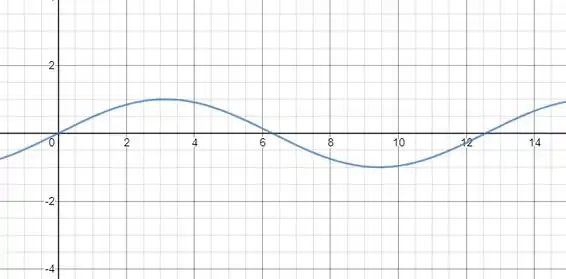
Passo 2

Nós podemos calcular alguns pontos para ajudar a esboçar o gráfico polar. Usando o incremento de , conseguimos os seguintes valores:

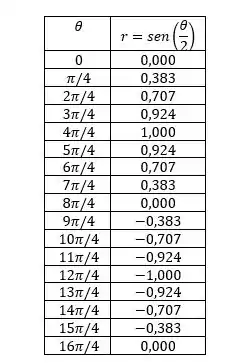
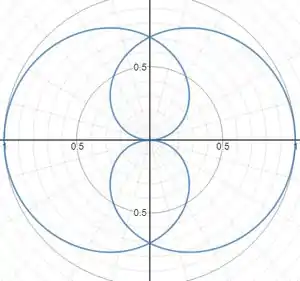
Do gráfico cartesiano e da tabela, nós podemos ver que uma cardioide é desenhada de a , com a parte maior para a esquerda.

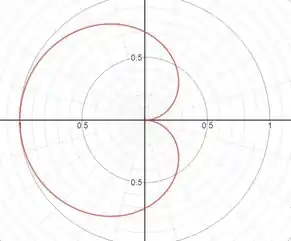
Já de a , por conta do valor negativo de , outra cardioide aparece com a parte maior para a direita.

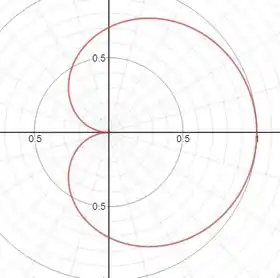
O desenho completo pode ser visto abaixo.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre equações paramétricas para a trajetória de uma partícula que se move ao longo do círculo x 2 + y - 1 2 = 4 Três vezes no sentido anti-horádio, a partir de ( 2,1 ) .

Encontre equações paramétricas para a trajetória de uma partícula que se move ao longo do círculo x 2 + y - 1 2 = 4 Uma vez no sentido horádio, a partir de ( 2,1 ) .

Trace a curvax = y - 3 y^3 + y^5

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.

Associe os gráficos das equações paramétricas x = f ( t ) y = g ( t ) Em a - ( d ) com as curvas paramétricas rotuladas de I - I V . Justifique.