Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 74
Use um gráfico para estimar a coordenada dos pontos mais altos na curva . Então, use o cálculo para encontrar o valor exato.
Passo 1
Fala galerinha. De boa? A questão nos pede para estimar a coordenada dos pontos mais altos na curva representada peça equação porlar utilizando um gráfico, e em seguida, encontrar o valor exato usando cálculo.
Segue os passo para resolvermos!
- Primeiro vamos gerar o gráfico dessa função utilizando uma ferramenta gráfica para visualizarmos a curva e estimarmos quais são os valores mais altos de .
- Para o cálculo exato teremos que encontrar as derivadas, a primeira e segunda, em relação a . O ponto crítico será encontrado onde a primeira derivada se anula, e a segunda derivada será para confirmar os pontos máximos locais.
Agora é só começar. Let’go!
Passo 2
Gráfico de
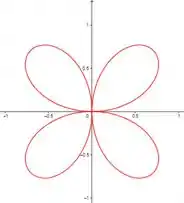
Olhando o gráfico dá pra concluirmos que o maior valor de está entre e . De olho eu diria que está próximo de .
Podemos também perceber que esses pontos estão no primeiro e segundo quadrante, ou no terceiro e quarto de forma negativa.
Passo 3
Para calcularmos os valores exatos agora, vamos calcular a derivada de
Iremos aplicar a regra do produto
Como
Passo 4
Substituindo o valor de
Pois quando temos uma inclinação horizontal, nos indicando um ponto crítico e então usamos a segunda derivada para acharmos os pontos de máximo e encontrarmos o maior valor de .
Para isso vamos calcular
Substituindo na equação
Passo 5
Igualando a zero para achar os pontos críticos
Substituindo e
Vamos substituir
Passo 6
Dando continuidade e fazendo a distributiva
Mudando de variável,
Colocando em evidência
Então podemos concluir que é uma raiz, para encontrar as outras raízes vamos fazer
Somando dos dois lados
Invertendo os lados
Dividindo por
Aplicando a raiz quadrada dos dois lados
Passo 7
Então os pontos críticos acontecem quando , e quando .
- Para
- Para
- Para , podemos manipular um pouco
Mas, sabemos que para esses valores não temos o máximo, basta olhar no gráfico.
Vamos chamar de , então
Passo 8
Multiplicando por
Como é uma função impar temos que , logo
Para isso temos
Temos também o seu suplementar
Passo 8
Então vamos ter que analisar esses ângulos:
Para saber quais são pontos de máximo, calculamos a segunda derivada e se ela for negativa o ponto é um ponto de máximo.
Passo 9
Agora pra aplicar os ângulos nessa função não tem jeito, pega uma calculadora e joga os valores. Para isso vamos usar uma aproximação de para jogar na calculadora .
Então os pontos de máximo são e .
Passo 10
Por fim vamos calcular o para esses valores.
Utilizando a calculadora novamente
A aproximação de foi até boa hehe.
Portanto o maior valor de para a função é .
Resposta
O maior valor de para a função é .