Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 29
Trace a curva
Passo 1
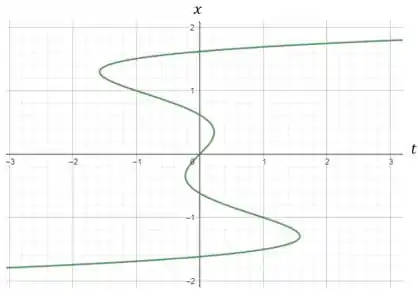
A questão pede pra gente traçar a seguinte curva com o auxílio de uma ferramenta gráfica:
Isso porque o livro considera útil ver um programa de computador traçando uma curva parametrizada.
Então primeiramente vamos transformar isso daí numa curva parametrizada.
Lembrando que a parametrização de uma curva é um processo usado para representar pontos na curva em termos de um ou mais parâmetros.
Assim, basicamente, vamos escolher adotar o parâmetro e definir uma função para esse parâmetro e, . Por fim, vamos aplicar em .
Agora bora lá!! 😉
Passo 2
Já temos que o nosso parâmetro é a variável .
Vamos criar uma função bem simples primeiramente:
Perceba que o parâmetro irá variar ao longo da curva, e os valores de serão simplesmente iguais aos valores de .
Então, substituindo na equação original pela função do parâmetro, temos:
Assim, podemos escrever a equação como o seguinte sistema de equações paramétricas:
Se plotarmos essa curva , teremos o seguinte resultado:
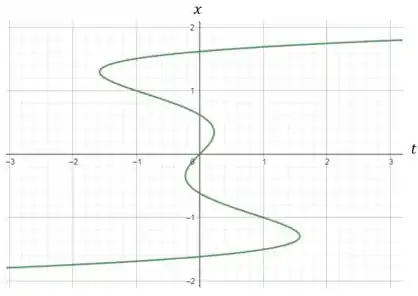
Resposta
