Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 66
Mostre que as curvas e se interceptam nos ângulos retos.
Passo 1
Olá, meu amigo. Vamos resolver juntos essa atividade.
Aqui a gente tem as curvas:
E
E queremos prova que quando elas se interceptam, isso acontece em um ângulo reto, isso é, ângulo de .
Se queremos mostrar que duas curvas se interceptam, a primeira coisa que precisamos fazer é igualar as duas equações para encontrar os ângulos em que eles se encontram.
Outro ponto em que elas vão se interceptar é na origem quando , que apesar de não existir um ângulo onde , a origem em si, o ponto, em coordenadas polares, é considerado um ponto de todas as angulações, como ele não tem distância, não tem diferença.
Logo, os pontos de intersecção dessa curva são e .
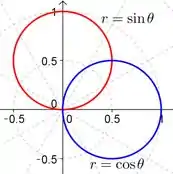
Então, o que iremos fazer aqui, depois de termos descoberto os pontos de interseção entre essas curvas em um ponto tangente delas, é descobrimos qual é o ângulo dessa tangencia, e como você bem sabe, tangencia e ângulo nos remete a derivadas.
Passo 2
Para descobrirmos o ângulo de intersecção vamos calcular a inclinação da tangente em cada ponto. Para isso, vamos usar a fórmula:
Para derivar as curvas vamos chamar de curva a curva
e de curva a curva
Vamos também chamar a inclinação da curva de e a inclinação da curva de . Então,
Fazendo umas simplificações trigonométricas com as relações e
Calculando agora a inclinação para a curva :
Fazendo umas simplificações trigonométricas com as relações e
Passo 3
Como vamos analisar também os pontos quando , precisamos encontrar para quais ângulos isso acontece nas curvas e .
Para curva :
Isso acontece quando e . Para a curva ,
Isso ocorre em e .
Passo 4
Por fim, vamos analisar as inclinações, para isso precisamos analisar pontos onde as curvas e tem ângulo e , além disso pontos onde as curvas tem .
Para
Mas calculando os limites laterais
Esses valores do limite indicam uma inclinação vertical.
Isso indica uma inclinação horizontal. Se temos em uma curva uma inclinação horizontal e na outra uma vertical, as duas se interceptam neste ponto com um ângulo reto.
Passo 5
Para
E como calculamos o limite em cima, sabemos que se trata de uma inclinação vertical.
Assim como para , temos uma inclinação vertical e outra horizontal, portanto se interceptam com ângulo reto.
Passo 6
Para , na curva com ângulos e temos uma inclinação
Então, sempre que a curva está na origem, sua inclinação é horizontal. Na curva com ângulos e
Analisando no limite
Temos para na curva uma inclinação vertical.
Para também temos uma inclinação vertical. Sempre que a curva está na origem, sua inclinação é vertical. Se para a curva tem inclinação horizontal e a curva vertical, elas se interceptam por ângulos retos.
O caminho foi longo, mas conseguimos, né? 😊
Resposta
Demonstração