Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 26

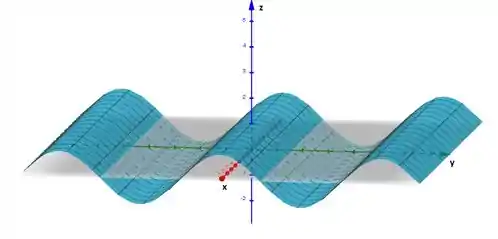
Esboce o gráfico da função.

f x , y = cos ⁡ y

Passo 1

Olá, meu querido amigo. Vou te ajudar a resolver essa atividade hoje.

Aqui iremos realizar o esboço do gráfico da função:

f x , y = cos ⁡ y

Para esboçarmos o gráfico de uma função de duas varáveis precisamos primeiramente encontrar as curvas de nível desta função.

Para isso façamos:

z = f x , y = cos ⁡ y

Então os valores de z , são dependentes da entrada de y . Veja que, por conta da função cosseno ser limitada em - 1 ≤ cos ⁡ y ≤ 1 , teremos também que - 1 ≤ z ≤ 1 .

Então devemos perceber que ao longo do eixo z , teremos uma oscilação entre - 1,1 .

Veja que por termos uma função de x , y mas o x não aparecer, indica que ele é x = 0 , sendo assim, nosso plano irá se estender de forma constante por todo o eixo x

Passo 2

Desta forma obtemos as seguintes curvas de nível:

z = 0

0 = cos ⁡ y

y = π 2

Para:

z = 1

1 = cos ⁡ y

y = 0

Para:

z = - 1

- 1 = cos ⁡ y

y = π

Temos então que nossa superfície de nível irá se repetir dessa forma:

Desta forma o gráfico de f x , y = cos ⁡ y é:

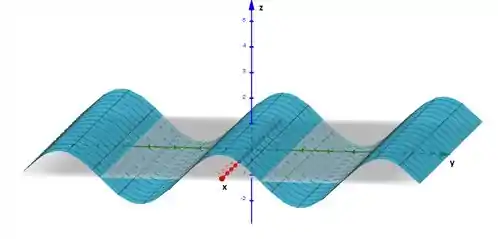
Como comentamos, o gráfico irá oscilar em z a partir de entradas de y e irá se estender por x

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f x , y = x x 2 + y 2 . Desenhe a imagem da curva γ t = ( x t , y t , z t ) , onde x t = Rc o s t ,y t = Rs e n t e z = f ( x , y ) (R0) . Como é o gráfico de f ?
10. Sejam f x , y = x yeγ t = a t , b t , f a t , b t . Desenhe a imagem de γ sendoa) a = 0 e b = 1 . b) a = 1 e b = 1 . c) a = 1 e b = 0 . d) a = - 1 e b = 1 .
Como é o gráfico de f (x , y) = x y ?
Duas curvas de nível podem se interceptar? Justifique.
12. Suponha que T x , y = 4 x 2 + 9 y 2 represente uma distribuição de temperatura no plano x y : T x , y é a temperatura, que podemos supor em °C, no ponto x , y . a) Desenhe a isoterma correspondent