Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 8
- Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta.
- Elimine o parâmetro para encontrar uma equação cartesiana da curva.
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade.
Aqui a gente tem a curva parametrizada:
E vamos criar o gráfico dessa curva marcando pontos em um gráfico. Para isso, a gente vai criar uma tabela, onde colocaremos valores de e seus respectivos valores de e , que são dependentes de .
Já na letra b), o que iremos fazer para colocarmos nossa curva em coordenadas cartesianas é isolar o valor de em uma das duas curvas, e substituirmos na outra.
Então podemos isolar o em e depois iremos colocar esse valor de em .
Passo 2
- Queremos esboçar a curva que tem as equações paramétricas dadas.
- Eliminando o parâmetro, temos que:
Bom, para isso, vamos criar uma tabelinha de valores que relacionam , e .
Aí poderemos plotar esses pontos no gráfico.
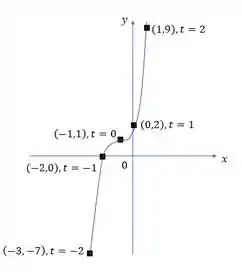
Assim, por exemplo, quando , teremos e .
E a curva que formamos com o auxílio do GeoGebra para plotarmos os pontos é a seguinte:
Veja que a medida que aumenta, tanto quanto aumentam de valor.
Passo 3
Isso implica que:
E então, sendo:
Iremos substituir o valor de aqui:
Agora a gente precisa encontrar o novo intervalo:
Então para :
E agora para :
Então nosso novo intervalo é:
