- Esboçe o gráfico de começando pelo gráfico de e usando as transformações da Seção .
- Use o gráfico da parte (a) para esboçar o gráfico de .
- Use a definição de derivada para encontrar . Quais os domínios de e ?
- Use um recurso gráfico para fazer o gráfico e compare-o com o esboço na parte (b).
Passo 1
Fala aí! tudo certinho? 😉

Nesse problema queremos esboçar o gráfico de começando pelo gráfico de e usando as transformações da Seção .
A partir daí queremos usar o gráfico da parte (a) para esboçar o gráfico de , usar a definição de derivada para encontrar e os domínios de e e por fim, a partir de uma calculadora gráfica, fazer o gráfico e comparar com o esboço na parte (b).
Parece complicado? 😁
Na seção 1.3 são dadas algumas propriedades de manipulação gráfica... como por exemplo de translação horizontal e vertical, rotação em função do eixo ou ...
Vamos usar essas propriedades para, apartir do gráfico de , esboçar o gráfico de .
Antes de começar de fato, vale relembrar a formulinha para obter
Tranquilo? Bora começar! 😇
Passo 2
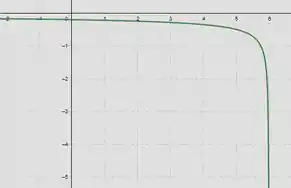
- Vamos lá, para usar as transformações da Seção vamos usar fazer primeiro o gráfico de :
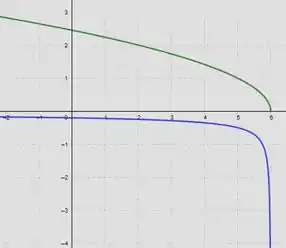
- Usando o gráfico da letra (a) esboçamos o gráfico da derivada.
- Vamos lá, para calcular pela definição vamos ter que relembrar a fórmula:
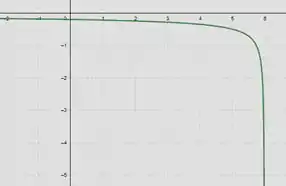
- Agora, como solicitado no enunciado, vamos plotar a função usando uma calculadora gráfica...
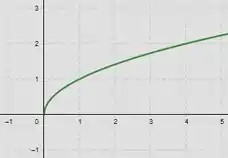
Vamos agora fazer o gráfico de : nesse caso, rotacionamos o gráfico em relação ao eixo , então o que era , agora será ...
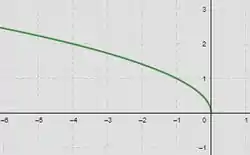
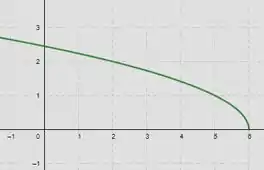
Vamos fazer o de : Perceba que virou , portanto fizemos uma translação horizontal de unidades para a direita...
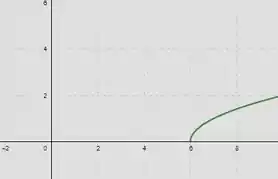
Agora vamos para o último, que é o que a gente quer, o de : Então rotacionamos com relação ao eixo novamente.
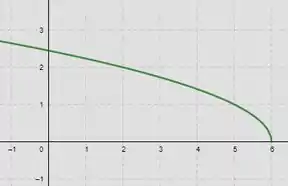
Bacana, não é? 😎
Passo 3
Perceba que quanto menor o , mais horizontal é o gráfico e portanto, nessa parte a inclinação/derivada é muito próximo de .
Mas depois que passa por a função começa a decrescer cada vez mais até que quando vai chegando próximo de a função decresce muito rapidamente e próximo a esse ponto a inclinação é quase vertical...
A partir daí, relacionando a inclinação da função à derivada, podemos esboçar o gráfico de como
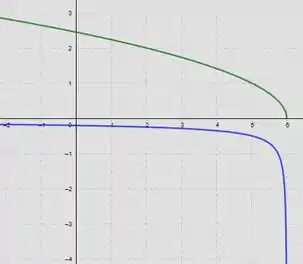
Tranquilo até aqui? 🤔
Passo 4
Ela parece complicada, mas só parece, temos que substituir com a função que queremos, vamos lá:
Se , temos
Vamos destrinchar esse numerador e ver se fica simples resolver, vamos devagar pra não cometer nenhum erro:
Agora calma, não se assuste, vamos fazer algumas manipulações e vai da tudo certo. Vamos multiplicar a expresão pelo conjugado do numerador, já que temos raíz alí no meio.
Assim, como , no numerador temos
Simplificando e no numerador, chegamos em
Agora podemos simplificar do numerador e do denominador.
Pronto, chegamos em uma expressão simples, agora é só resolver aplicadando o valor que tende:
Bora continuar! 😊
Passo 5
Agora vamos ver os domínios das duas funções: O domínio da função nada mais é do que o conjunto de valores que sua variavel pode assumir para que a função exista...
A função tem uma raíz, então a expressão dentro dela deve ser maior ou igual a , assim devemos ter que
então o domínio é.
Já com a derivada da função, , temos o domínio o domínio muito parecido, aqui além de também termos a raíz tendo a mesma limitação de , temos no denominador, o que nos impede do valor assumir , pois isso nos faria ter um denominador igual a .
Portanto o domínio de é
Interessante, não é? 👀
Passo 6
E aí! o que achou? Responde Aí! 😬
Resposta